多变量
多变量的定义
预测房价的例子,一个变量不足以描述对房价的影响时,需要多个变量共同决定决定房屋的价值,如面积/房间数/年限等。
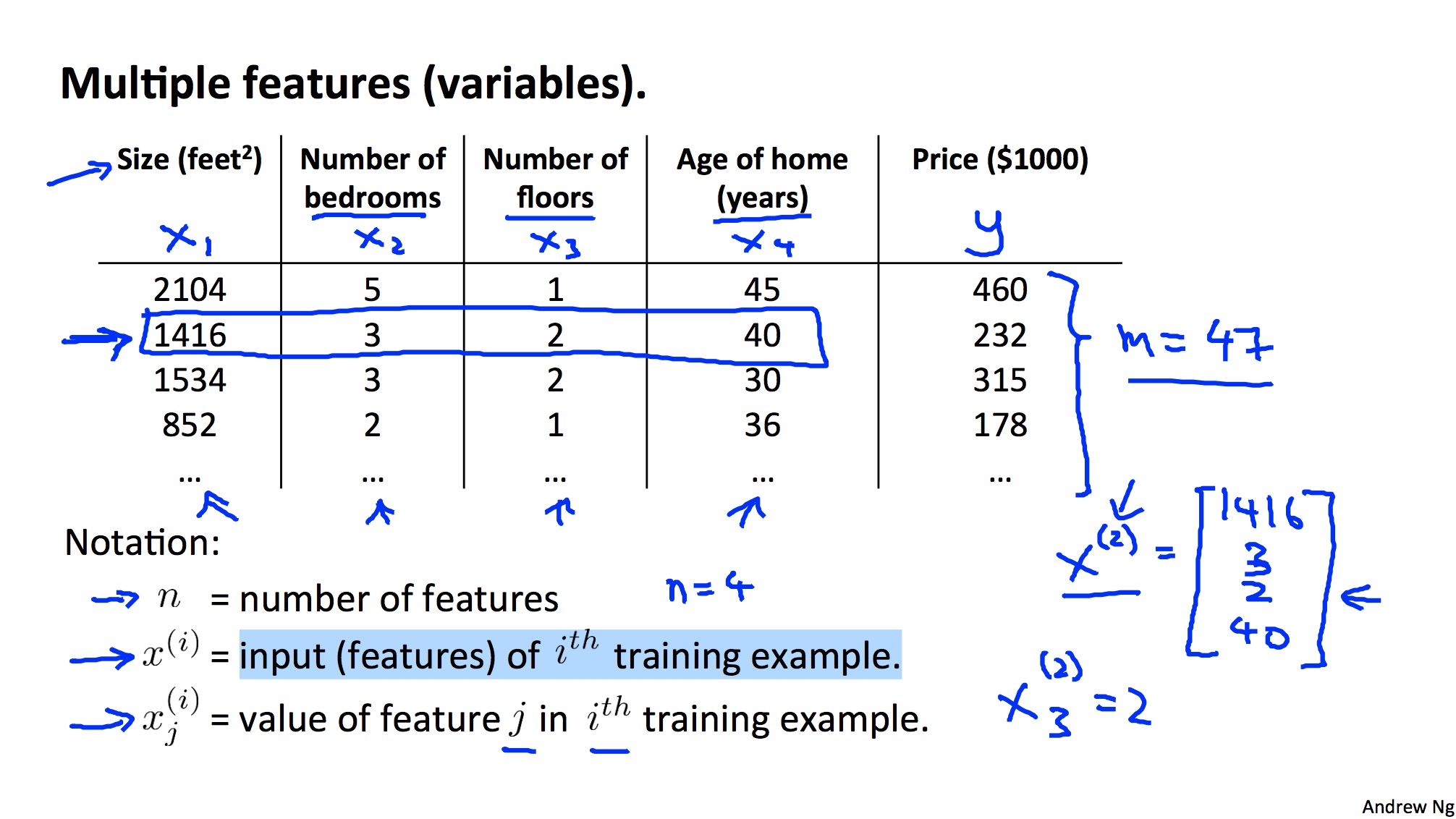
对应的Hypothesis函数也就强化为所有变量的函数。将上一章的函数扩展,并将x0默认为1,可以得到Hypothesis函数的矩阵数学表示,即theta向量的逆和X向量的乘。

多变量的梯度下降法
由单变量扩展来,多变量的梯度下降法在每次迭代的时候需要同步更新所有变量对应的theta(0/1/。。。/n),数学公式跟之前没有大的差别。

Feature Scaling
多变量带来一个问题,就是不同变量的取值范围可能差异很大。为了将所有变量缩放到一个统一的范围,以加速迭代收敛,引入了Mean normalization(均值归一化)。用训练集中每个变量的均值和范围来重新归一化每个变量。

Learning rate
梯度下降法里面一个重要的参数alpha,怎么选择呢?如果alpha太小,会导致收敛过慢;如果alpha太大,则可能会导致J(theta)无法在每次迭代都能下降,最终可能无法收敛。如下是一种选择alpha的方法:

Normal equation
梯度下降法使用起来比较麻烦,因为需要指定theta的初始值,还需要选择alpha,做feature scaling等等。现在引入Normal equation,在特定场景下可以更方便地求theta。
Normal equation的推导:

什么情况下可以用Normal equation?在样本不是太大的时候,因为样本太大时矩阵的计算十分耗时。

