手机阅读会有问题-。=
之前用 Tensorflow 提供的目标识别库做了图像识别,那只是借花献佛。如何自己使用 Tensorflow 实现图像识别(本文具体来说是识别交通标志)?如何自己用训练数据训练出神经网络模型?如何提高模型的准确性?开搞!
最最基础
机器学习到底做什么事情?
回顾之前的文章机器学习的学习1:model和cost function,了解最基本的输入输出模型及损失函数。简单来说机器学习处理的问题分为回归问题和分类问题。
有监督的图像识别做什么事情?
实际上就是个分类问题,把图像判定为某种物体或者标识。具体到识别交通标志这件事情上,就是把图像判定为某种交通标志。我们这个案例共有62种交通标志,就是说拿到一个图像,判断它符合哪个标志的概率最大,则将其分类到该标志下。
有监督是指什么?是指我们的样本里不仅仅有数据源,并且还已经人为打上了标签,即我们已经知道了它属于某种交通标志。相对应的,无监督是指只有数据源,而不知道它的标签(类别)。
最终到底要计算什么?
机器学习通过建模,将输入(图像)和输出(判定的标志)映射起来,这个映射函数包含「权重(weights)」和「偏差(bias)」,需要在不断的训练中找到最优值。这个映射函数就是对真实世界某个场景的模拟。
数学表达式很简单:Y = X * W + b
怎么判断系统的优劣?
如果系统除了训练数据以外还提供了测试数据,那么可以直接利用测试数据,通过判定的准确度来判定权重和偏差是好是坏。如果没有提供测试数据,那就想其他办法吧。。。
我们要做的,就是利用不同的模型,找到对应最优的权重和偏差,讲最终的准确度提高到最大值。
单层神经网络
开始了本文的重点。我们先尝试最简单的模型,即单层神经网络。一般来说,神经网络层数越多(越深层)其力量越大。但这不代表单层神经网络没有其用武之地了。
一个简化的单层神经网络如下图
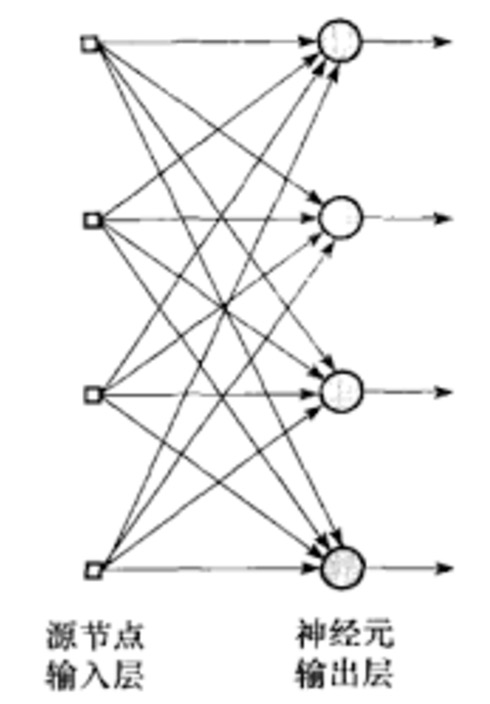
图像预处理
为了建立模型,需要对图像统一处理,将所有图像resize为 28*28 像素的图像。再者图像的颜色对本案例的意义不大,故用PIL的convert(‘L’) 做了颜色的单一化。
原图像为下图:

转为下图:

对所有图像都进行如上的处理,训练数据共 4575 张,测试数据为 2520 张。
输入输出模型
经过预处理之后,一张图像就被 28*28=784 个像素点给代表了,即输入层为 784 个。输出层为 0 到 61 共 62 个神经元,代表 62 种分类类型。通过「全连接」连接起来的。

神经网络中的每个「神经元」对其所有的输入进行加权求和,并添加一个被称为「偏置(bias)」的常数,然后通过一些非线性激活函数来反馈结果。
激活函数和softmax
激活函数用于给神经网络加入非线性因素的,因为线性模型的表达能力不够。对于分类问题,softmax 是一个不错的激活函数。通过取每个元素的指数,然后归一化向量(使用任意的范数(norm),比如向量的普通欧几里得距离)从而将 softmax 应用于向量。

那么为什么「softmax」会被称为 softmax 呢?指数是一种骤增的函数。这将加大向量中每个元素的差异。它也会迅速地产生一个巨大的值。然后,当进行向量的标准化时,支配范数(norm)的最大的元素将会被标准化为一个接近 1 的数字,其他的元素将会被一个较大的值分割并被标准化为一个接近 0 的数字。所得到的向量清楚地显示出了哪个是其最大的值,即「max」,但是却又保留了其值的原始的相对排列顺序,因此即为「soft」。
矩阵计算
我们现在将使用矩阵乘法将这个单层的神经元的行为总结进一个简单的公式当中。使用加权矩阵 W 的第一列权重,我们计算第一个图像所有像素的加权和。该和对应于第一神经元。使用第二列权重,我们对第二个神经元进行同样的操作,直到第 62 个神经元。然后,我们可以对剩余的图像重复操作。如果我们把一个包含 100 个图像的矩阵称为 X,那么我们的 62 个神经元在这 100 张图像上的加权和就是简单的 X * W(矩阵乘法)。
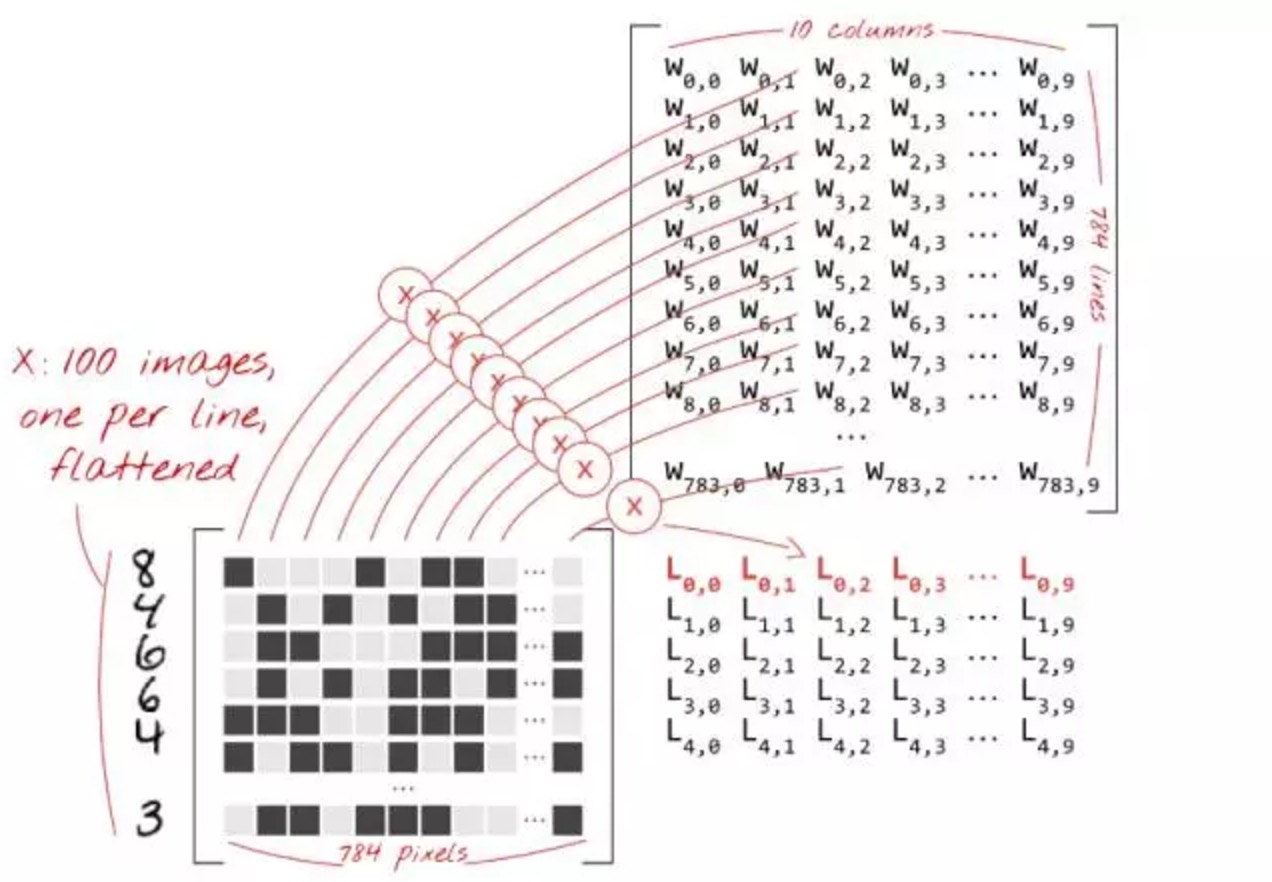
每一个神经元都必须添加其偏置(一个常数)。因为我们有 62 个神经元,我们同样拥有 62 个偏置常数。我们将这个 62 个值的向量称为 b。它必须被添加到先前计算的矩阵中的每一行当中。使用一个称为 “broadcasting” 的魔法,我们将会用一个简单的加号写出它。
我们最终应用 softmax 激活函数并且得到一个描述单层神经网络的公式,并将其应用于 100 张图像:

特别说明:上文(包括图片中)提到的 100 张图像是一个 mini-batch 的概念,实际上在本案例的运算中是将 4575 张图片一起投入计算,使得输入是一个 4575 * 784 的矩阵。究其原因,是因为训练数据是按照其分类排好序的,如果按 mini-batch 投入运算,会每个迭代对这 100 张图像过拟合,最终使参数左右摇摆。如果要用到 mini-batch,需要将数据源顺序打乱。
这部分代码:
BATCH_NUM = 4575
TAEGET_NUM = 62
# input X: 28x28 grayscale images, the first dimension (None) will index the images in the mini-batch
X = tf.placeholder(tf.float32, [None, 28, 28, 1])
# correct answers will go here
Y_ = tf.placeholder(tf.float32, [None, TAEGET_NUM])
# weights W[784, TAEGET_NUM] 784=28*28
W = tf.Variable(tf.zeros([784, TAEGET_NUM]))
# biases b[TAEGET_NUM]
b = tf.Variable(tf.zeros([TAEGET_NUM]))
# flatten the images into a single line of pixels
# -1 in the shape definition means "the only possible dimension that will preserve the number of elements"
XX = tf.reshape(X, [-1, 784])
# The model
Y = tf.matmul(XX, W) + b
- 上述代码定义 TensorFlow 的变量和占位符。变量是你希望训练算法为你确定的所有的参数。在我们的例子中参数是权重和偏差。
- 占位符是在训练期间填充实际数据的参数,通常是训练图像。占位符 X 持有训练图像的张量的形式是 [None, 28, 28, 1],其中的参数代表:28, 28, 1: 图像是 28x28 每像素 x 1(灰度)。最后一个数字对于彩色图像是 3 但在这里并非是必须的。None: 这是代表图像的数量。在训练时可以得到。
- 最后一行是我们单层神经网络的模型。公式是我们在前面的理论部分建立的。tf.reshape 命令将我们的 28×28 的图像转化成 784 个像素的单向量。在 reshape 中的「-1」意味着「计算机,计算出来,这只有一种可能」。
- 占位符 Y 用于训练标签,这些标签与训练图像一起被提供。
如上就是该单层网络的“静态部分”,然后是“动态部分”。
迭代和梯度下降
上文提到过,为了判断模型的优劣,需要计算模型的精确度。我们用「判定结果」(即上文的Y)和「自有标签」(见下文的Y_)的距离来描述模型的精确程度。任何一种定义的距离都可以进行这样的操作,普通欧几里得距离是可以的,但是对于分类问题,被称为「交叉熵(cross-entropy)」的距离更加有效。

交叉熵是一个关于权重、偏置、训练图像的像素和其已知标签的函数。
不断迭代
「训练」一个神经网络实际上意味着使用训练图像和标签来调整权重和偏置,以便最小化交叉熵损失函数。通过不断的迭代,使得计算的权重和偏置不断优化。
梯度下降
关于梯度下降,可以参考之前的文章机器学习的学习1:model和cost function。
总结一下,以下是训练过程的步骤:
训练数字和标签 => 损失函数 => 梯度(部分偏导数)=> 最陡的梯度 => 更新权重和偏置 => 使用下一个迭代重复这一过程
这部分代码:
# cross-entropy
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=Y_, logits=Y))
# accuracy of the trained model, between 0 (worst) and 1 (best)
predict = tf.argmax(Y, 1)
correct_prediction = tf.equal(predict, tf.argmax(Y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# training, learning rate = 0.005
train_step = tf.train.GradientDescentOptimizer(0.005).minimize(cross_entropy)
- 代码使用softmax_cross_entropy_with_logits内置函数计算交叉熵
- 使用tf.train.GradientDescentOptimizer表示梯度下降的训练
运行Tensorflow
运算模型
上文在 Tensorflow 中都是模型的建立部分,终于来到了运行部分。
TensorFlow 的 “延迟执行(deferred execution)” 模型:TensorFlow 是为分布式计算构建的。它必须知道你要计算的是什么、你的执行图(execution graph),然后才开始发送计算任务到各种计算机。这就是为什么它有一个延迟执行模型,你首先使用 TensorFlow 函数在内存中创造一个计算图,然后启动一个执行 Session 并且使用 Session.run 执行实际计算任务。在此时,图形无法被更改。
由于这个模型,TensorFlow 接管了分布式运算的大量运筹。例如,假如你指示它在计算机 1 上运行计算的一部分 ,而在计算机 2 上运行另一部分,它可以自动进行必要的数据传输。
计算需要将实际数据反馈进你在 TensorFlow 代码中定义的占位符。这是以 Python 的 dictionary 的形式给出的,其中的键是占位符的名称。
这部分代码:
# init
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
# You can call this function in a loop to train the model, 100 images at a time
def training_step(i, update_test_data, update_train_data):
batch_X, batch_Y = train.next_batch(BATCH_NUM)
if len(batch_X) == 0:
return
# compute training values for visualisation
if update_train_data:
a, c = sess.run([accuracy, cross_entropy], feed_dict={X: batch_X, Y_: batch_Y})
print(str(i) + ": accuracy:" + str(a) + " loss: " + str(c))
# compute test values for visualisation
if update_test_data:
test_X, test_Y = test.next_batch()
a, c = sess.run([accuracy, cross_entropy], feed_dict={X: test_X, Y_: test_Y})
print(str(i) + ": ********* epoch " + " ********* test accuracy:" + str(a) + " test loss: " + str(c))
# the backpropagation training step
sess.run(train_step, feed_dict={X: batch_X, Y_: batch_Y})
for i in range(200+1):
training_step(i, i % 100 == 0, i % 10 == 0)
运算结构
可以看到准确度(accuracy)在逐步提升:
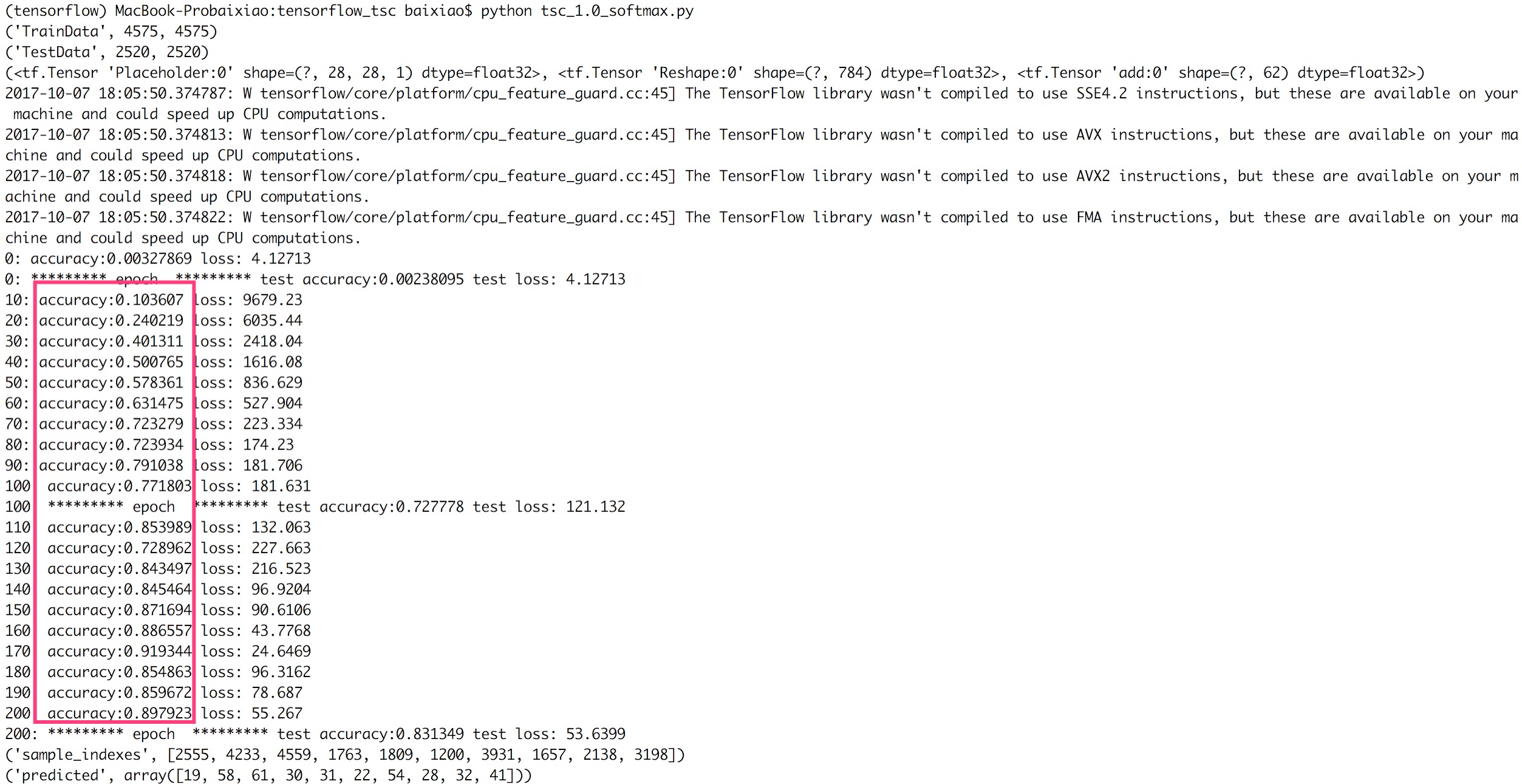
抽取10个训练样本,感性地看看整体模型的效果:
# 运行模型
# Pick 10 random images
sample_indexes = random.sample(range(len(train.images)), 10)
print("sample_indexes", sample_indexes)
sample_images = [train.images[i] for i in sample_indexes]
sample_labels = [train.labels[i] for i in sample_indexes]
# Run the "predicted_labels" op.
predicted = sess.run([predict], feed_dict={X: sample_images})[0]
# Print the real and predicted labels
# print(sample_labels)
print("predicted", predicted)
# Display the predictions and the ground truth visually.
fig = plt.figure(figsize=(10, 10))
for i in range(len(sample_images)):
truth = np.argmax(sample_labels[i])
# print(truth, sample_labels[i])
prediction = predicted[i]
plt.subplot(5, 2, 1+i)
plt.axis('off')
color = 'green' if truth == prediction else 'red'
plt.text(40, 10, "Truth: {0}\nPrediction: {1}".format(truth, prediction),
fontsize=12, color=color)
plt.imshow(sample_images[i].reshape(28,28))
plt.show()

增加训练迭代次数
迭代增加为1000次,训练数据拟合的更好,测试数据的精确度并没有提升:
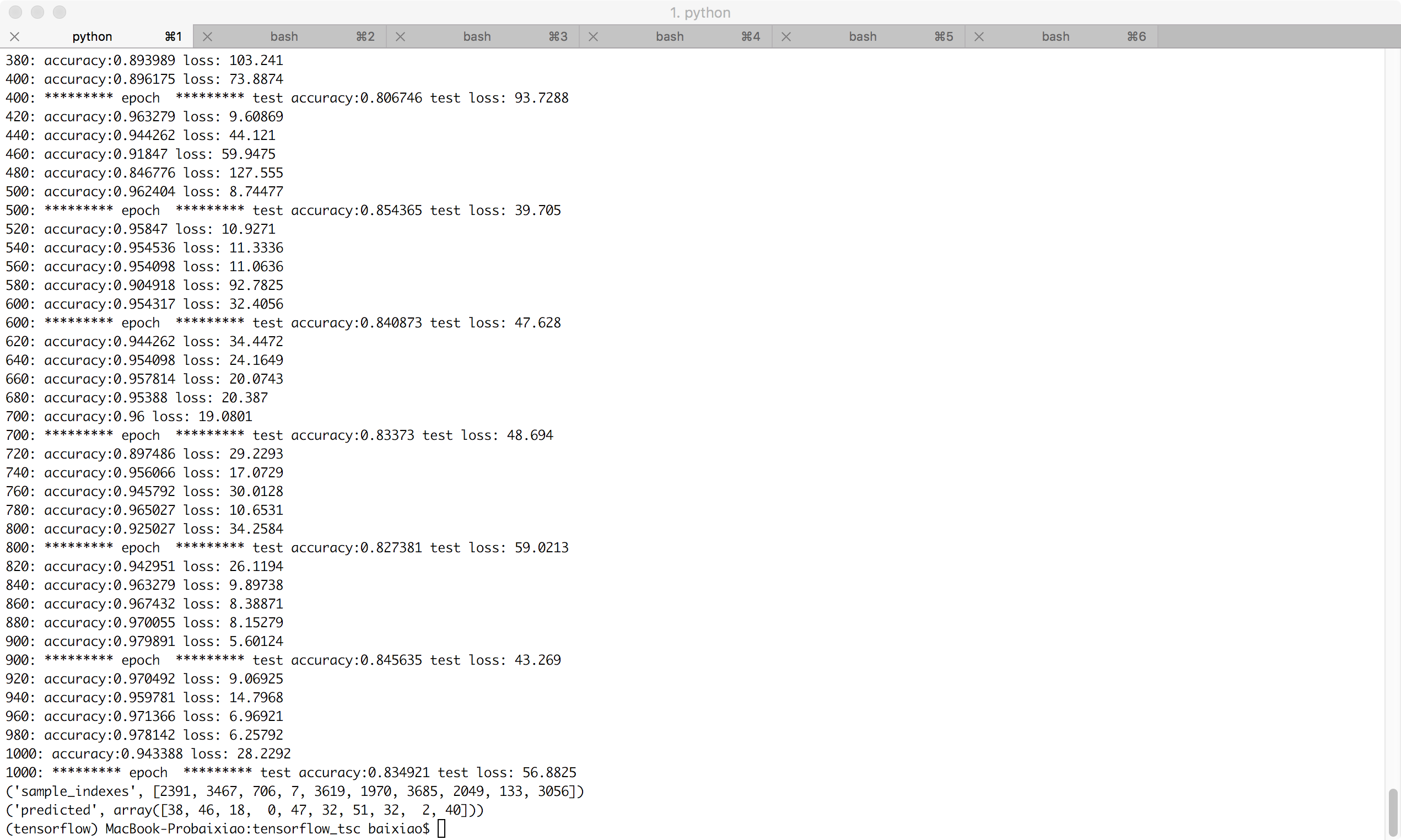
结束
完整代码在https://github.com/baixiaoustc/tensorflow_tsc/blob/master/tsc_1.0_softmax.py
参考:
