手机阅读会有问题-。=
本文在前文的基础上,继续提升图像识别的准确度。
优化器
众多优化器
Tensorflow提供了很多优化器,前文使用的tf.train.GradientDescentOptimizer,就是梯度下降的优化器。除此之外,还有其他算法的优化器如Momentum/Adagrad/Adadelta/Adam(Adaptive Moment Estimation)等。
如下是Tensorflow提供的优化器
- tf.train.GradientDescentOptimizer
- tf.train.AdadeltaOptimizer
- tf.train.AdagradOptimizer
- tf.train.MomentumOptimizer
- tf.train.AdamOptimizer
梯度下降的缺点
先复习一下梯度下降的公式:
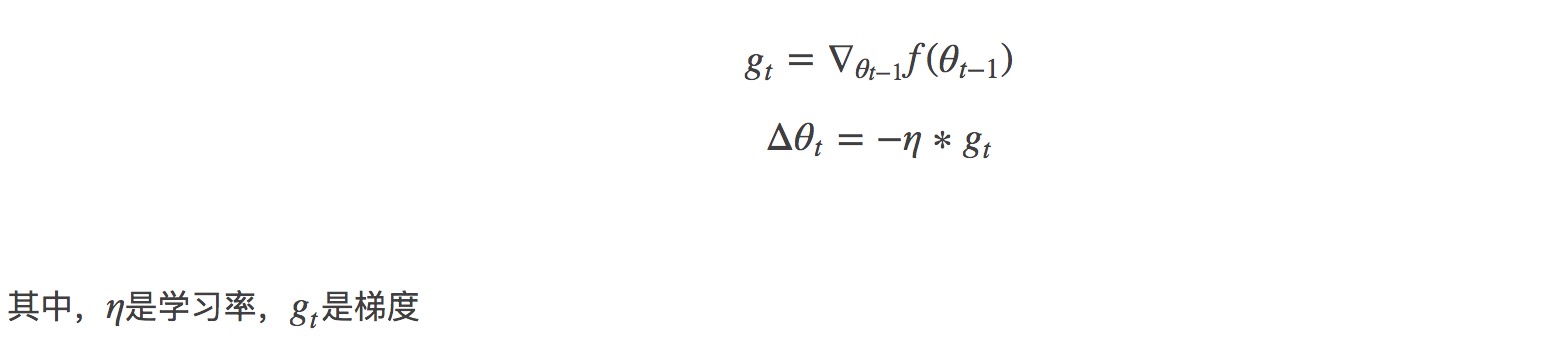
「学习率(learning rate)」: 在整个梯度的长度上,你不能在每一次迭代的时候都对权重和偏置进行更新。这就会像是你穿着七里靴却试图到达一个山谷的底部。你会直接从山谷的一边到达另一边。为了到达底部,你需要一些更小的步伐,即只使用梯度的一部分,通常在 1/1000 区域中。我们称这个部分为「学习率(Learning rate)」。
- 学习率的选择是一个难点。如果选择的太小,收敛速度会很慢,如果太大,loss function 就会在极小值处不停地震荡甚至偏离。
- 此外,这种方法是对所有参数更新时应用同样的学习率,如果我们的数据是稀疏的,我们更希望对出现频率低的特征进行大一点的更新。
- 对于非凸函数,还要避免陷于局部极小值处,或者鞍点处。鞍点如下图所示:
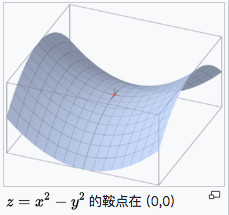
为了应对上述这三点挑战,于是就有了下面这些算法。
Momentum
momentum是模拟物理里动量的概念,积累之前的动量来替代真正的梯度。公式如下:

特点:
- 下降初期时,使用上一次参数更新,下降方向一致,乘上较大的μ能够进行很好的加速。
- 下降中后期时,在局部最小值来回震荡的时候,gradient→0,μ使得更新幅度增大,跳出陷阱。
- 在梯度改变方向的时候,μ能够减少更新。
Adagrad
Adagrad其实是对学习率进行了一个约束。即:

特点:
- 前期gt较小的时候,regularizer较大,能够放大梯度。
- 后期gt较大的时候,regularizer较小,能够约束梯度。
- 适合处理稀疏梯度。
Adam
Adam(Adaptive Moment Estimation)本质上是上述方法的结合进一步优化。公式如下:
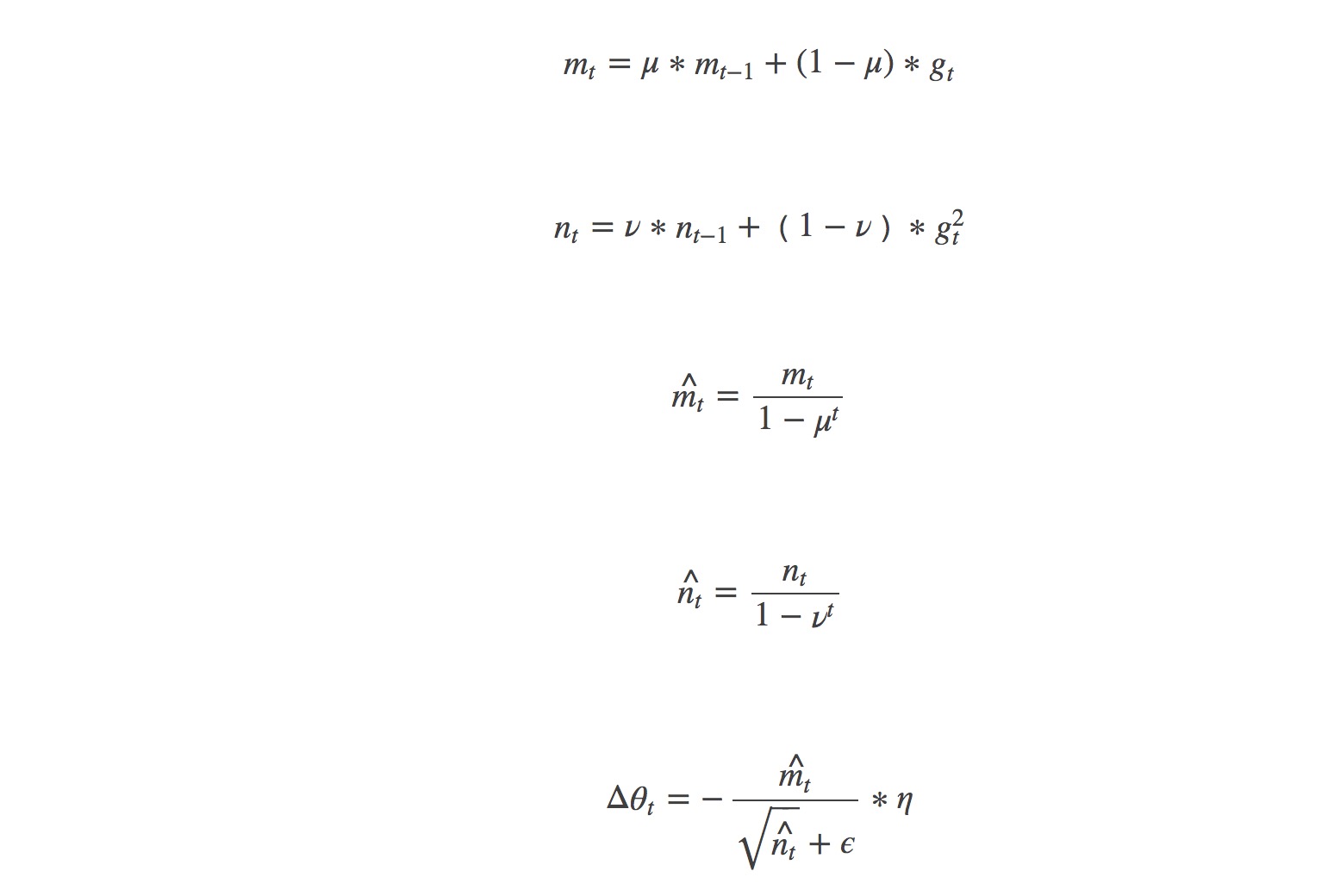
特点:
- 对内存需求较小。
- 为不同的参数计算不同的自适应学习率。
- 也适用于大多非凸优化。
- 适用于大数据集和高维空间。
实战
在前文的基础上,将优化器替换为Adam,故训练步骤为:
# training, learning rate = 0.003
train_step = tf.train.AdamOptimizer(0.003).minimize(cross_entropy)
200次迭代的adam优化器,准确度均有提升:
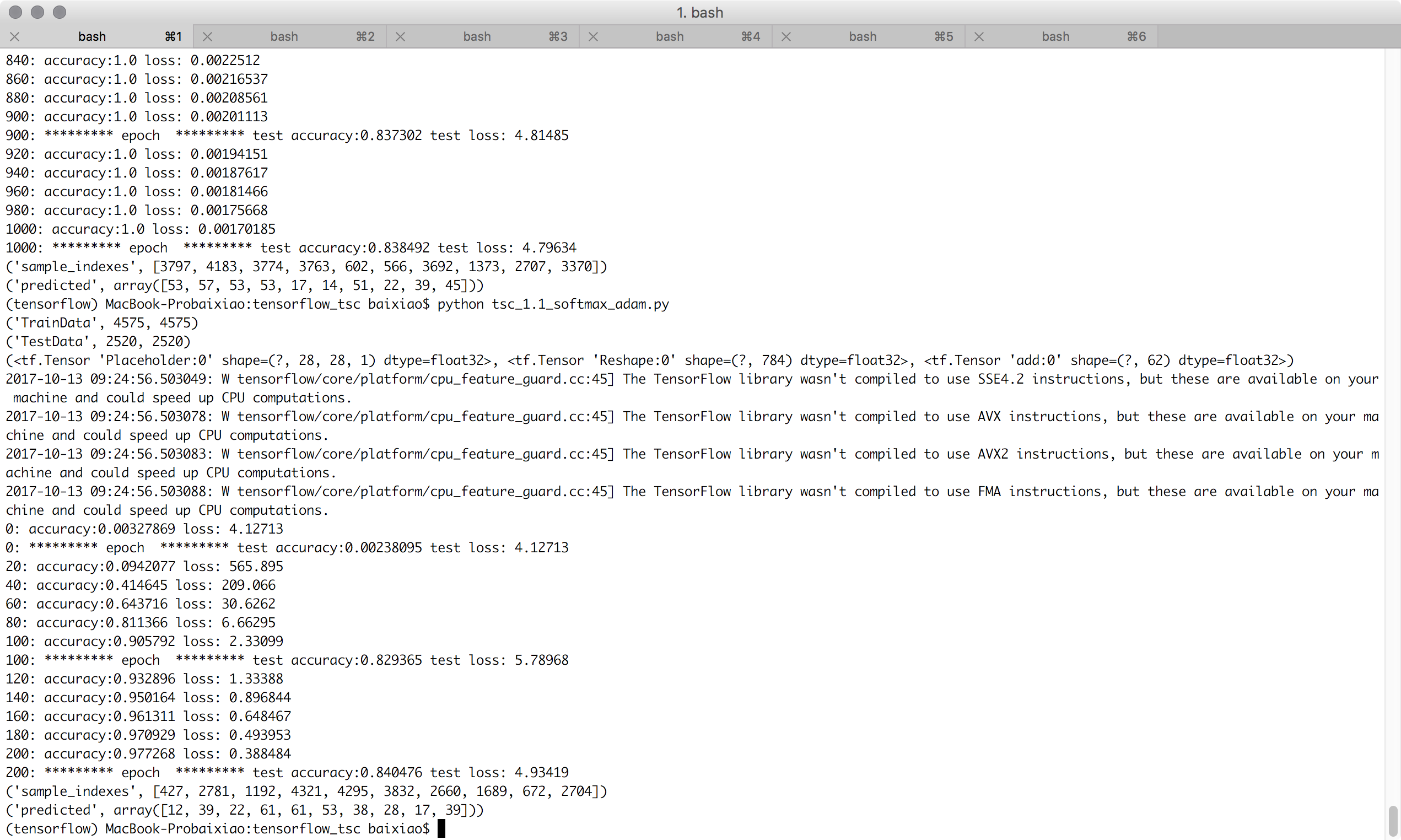
1000次迭代的adam优化器,居然训练数据准确度达到100%:
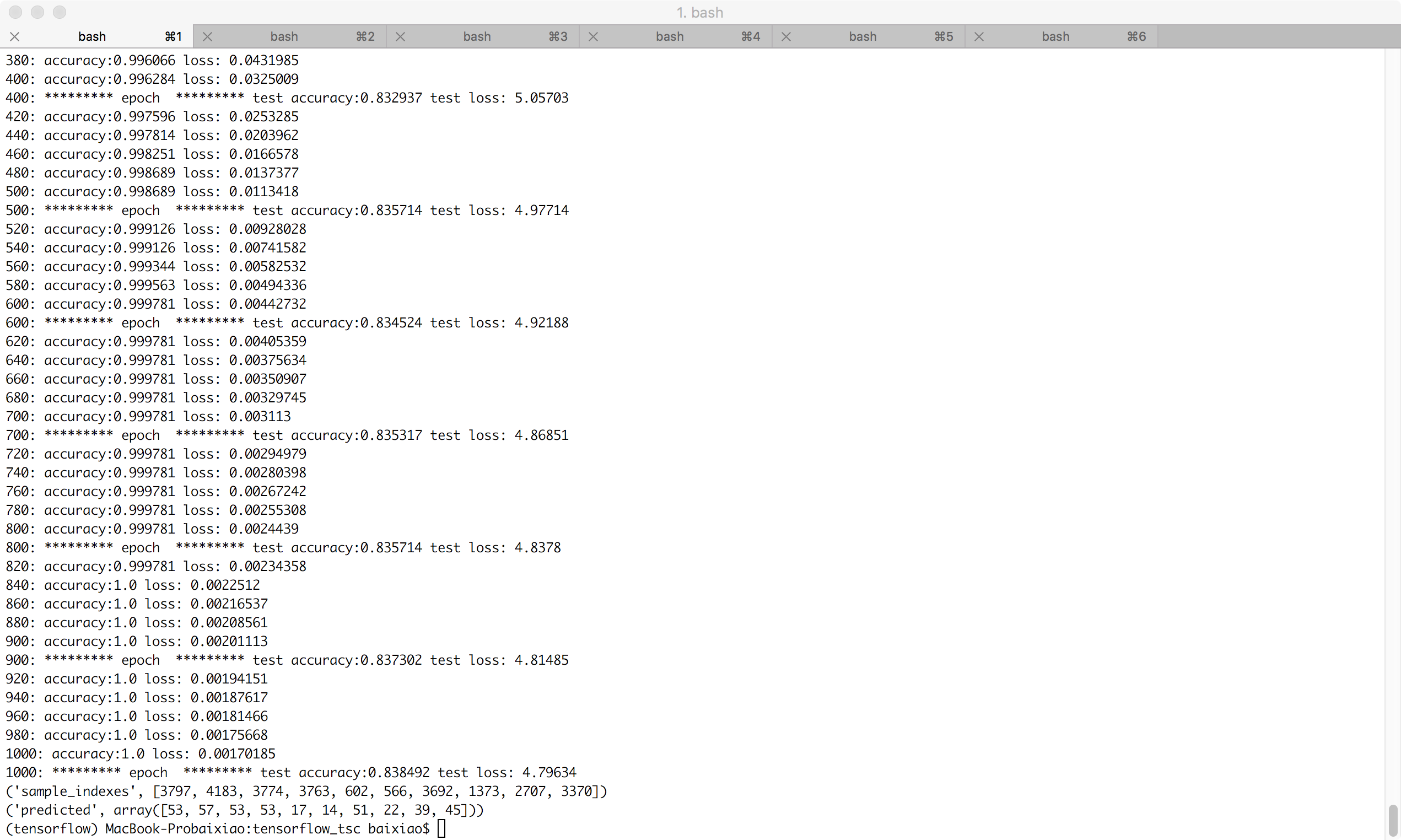
结束
完整代码在https://github.com/baixiaoustc/tensorflow_tsc/blob/master/tsc_1.1_softmax_adam.py
参考:
