手机阅读会有问题-。=
本文在前文的基础上,引入深层神经网络来继续提升图像识别的准确度。
神经元的激活
神经元结构
先复习一下单层神经网络的基础知识。
我们知道计算机神经网络是模拟人脑的结构,人脑的基本计算单元叫做神经元。下图粗略地描绘了一下人体神经元与我们简化过后的数学模型。在基本生物模型中,每个神经元都从多个树突接受信号,同时顺着轴突传递信号,轴突上有很多轴突末梢和其他的神经元树突连接。树突传导信号到神经元细胞,然后这些信号被加和在一块儿了,如果加和的结果被神经元感知超过了某种阈值,那么神经元就被激活,同时沿着轴突向下一个神经元传导信号。在我们简化的数学计算模型中,我们假定有一个『激活函数』来控制加和的结果对神经元的刺激程度,从而控制着是否激活神经元和向后传导信号。
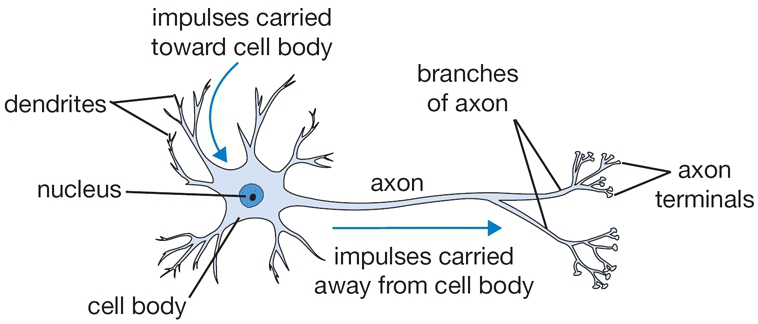
而我们可以看到下边简化的神经元计算模型中,信号也是顺着树突(比如x0)传递,然后在轴突处受到激励(w0倍)然后变成w0x0。我们可以这么理解这个模型:在信号的传导过程中,突触可以控制传导到下一个神经元的信号强弱(数学模型中的权重w),而这种强弱是可以学习到的。
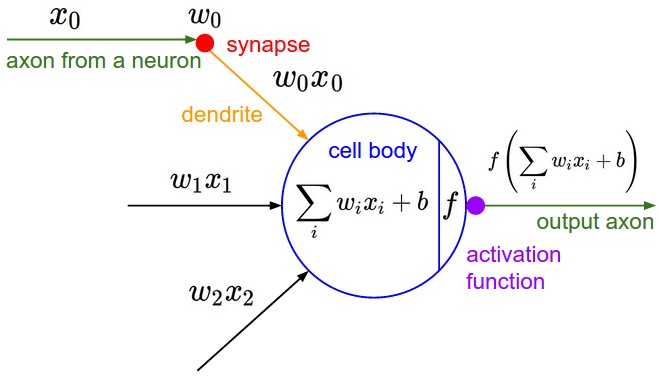
事实上,神经网络的本质就是通过参数与激活函数来拟合特征与目标之间的真实函数关系。因此,选择激活函数(activation function)成为了问题的一个难点。
激活函数
Sigmoid
Sigmoid函数曾被广泛地应用,但由于其自身的一些缺陷,现在很少被使用了。Sigmoid函数总会输出一个0-1之间的值,我们可以认为这个值表明信号的强度、或者神经元被激活的概率。Sigmoid函数被定义为:

函数对应的图像是:
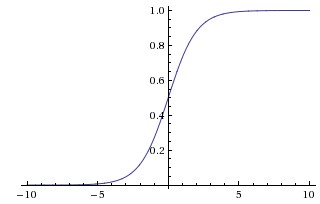
其对x的导数可以用自身表示:
比如说,我们在逻辑回归中用到的sigmoid函数就是一种激励函数,因为对于求和的结果输入,
优点:
- Sigmoid函数的输出映射在(0,1)(0,1)之间,单调连续,输出范围有限,优化稳定,可以用作输出层。
- 求导容易。
缺点:
- 由于其软饱和性,容易产生梯度消失,导致训练出现问题。
- 其输出并不是以0为中心的。
深层网络
神经网络的历史
回顾历史,从单层神经网络(感知器)开始,到包含一个隐藏层的两层神经网络,再到多层的深度神经网络,一共有三次兴起过程:
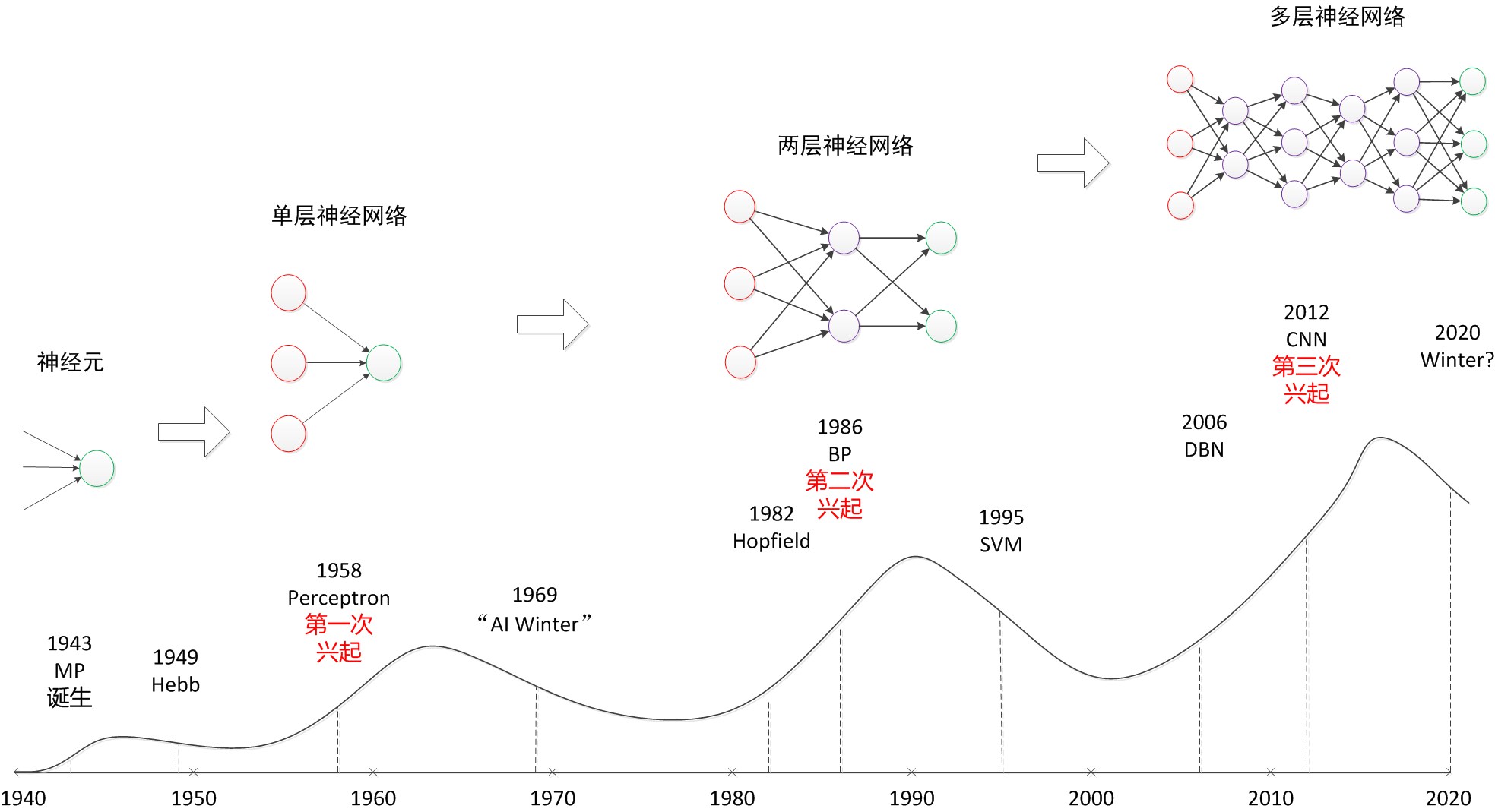
从图可见,目前正处于神经网络第三次兴起的阶段。但万事无常,这波热潮过去后说不定又要进入冷却期。只有期待量子计算带来的计算能力提高,或是又有革命性的算法出来,才有可能将神经网络应用到更加广泛的场景。
层级连接的结构
之前用到的是单层神经网络,现在说说普遍的结构。神经网络的结构是一种单向的层级连接结构,每一层可能有多个神经元。再形象一点说,就是每一层的输出将会作为下一层的输入数据。一般情况下,单层内的这些神经元之间是没有连接的。最常见的一种神经网络结构就是全连接层级神经网络,也就是相邻两层之间,每个神经元和每个神经元都是相连的,单层内的神经元之间是没有关联的。一般从前往后分为输入层/隐藏层/输出层。只有输入层和输出层的时候就为单层网络。注意命名习俗里面,通常是不把输入层计算在层数内的。
2层神经网络:
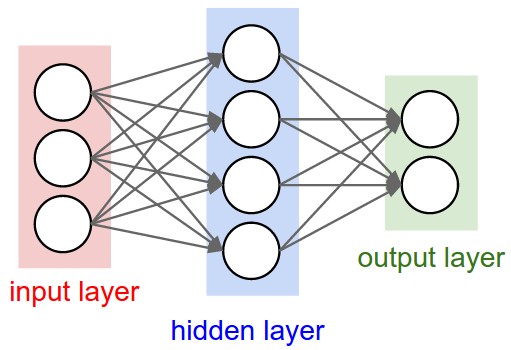
3层神经网络:
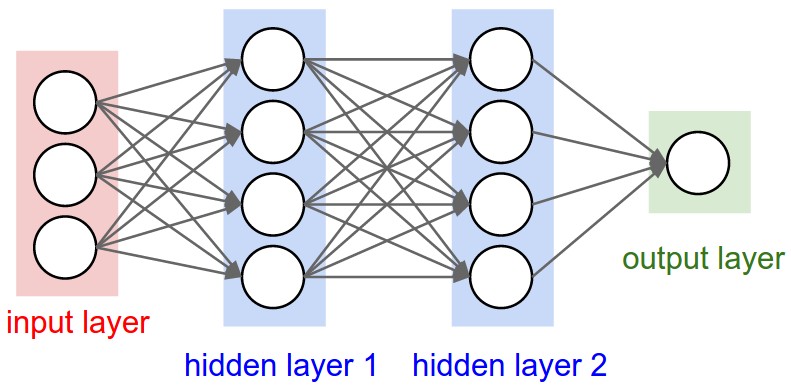
我们想想为什么需要多层网络?因为单层网络不管再怎么说,Y = X * W + b,这都是一个线性函数,无法完美地拟合真实情况。而多层网络加上激活函数引入的非线性特征,才是解决问题的关键。
实战
增加隐藏层

为了提高识别的准确度,我们将为神经网络增加更多的层。第二层神经元将计算前一层神经元输出的加权和,而非计算像素的加权和。这里有一个 5 层全相连的神经网络的例子:
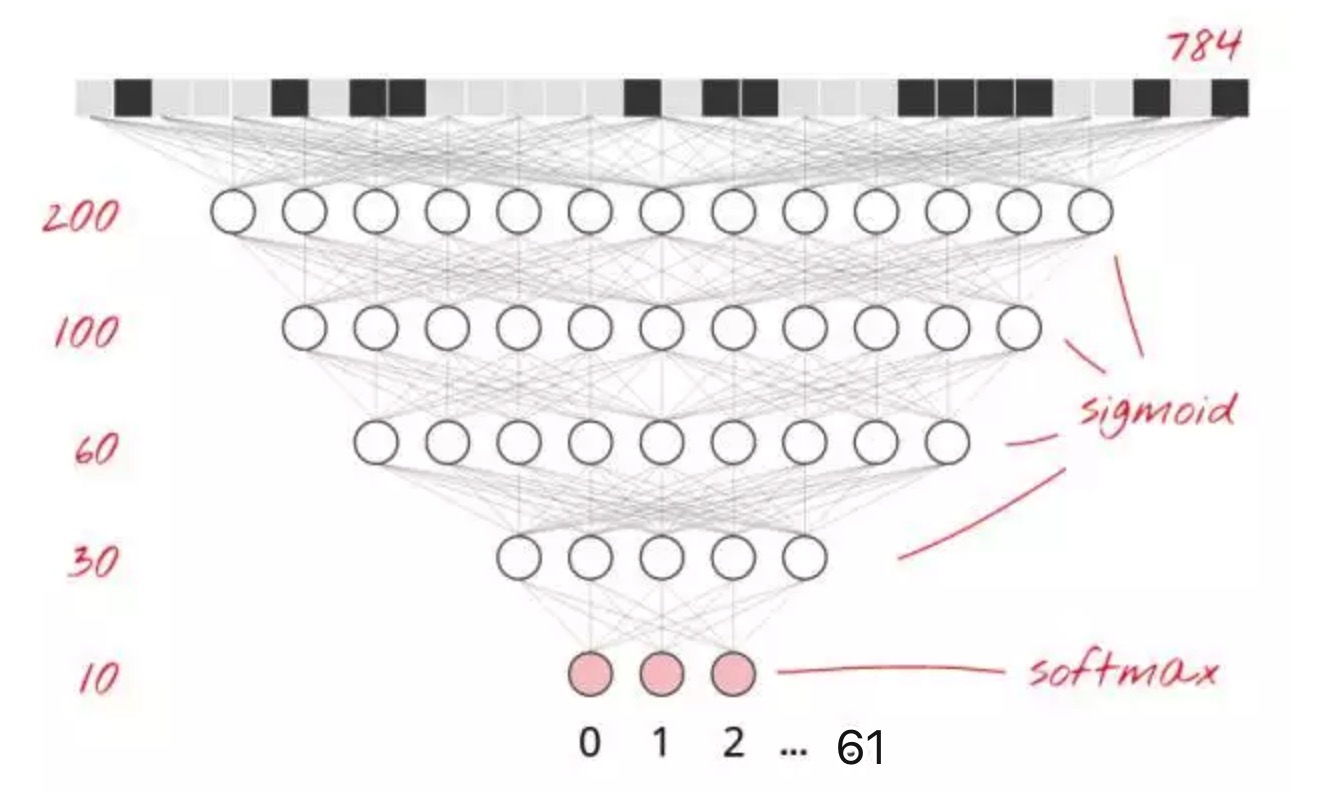
我们继续用 softmax 来作为最后一层的激活函数,这也是为什么在分类这个问题上它性能优异的原因。但在中间层,我们要使用最经典的激活函数:sigmoid。实际中,我们只使用了一个三层的神经网络,代码:
L = 300
M = 150
# N = 100
# O = 80
# Weights initialised with small random values between -0.2 and +0.2
W1 = tf.Variable(tf.truncated_normal([784, L], stddev=0.1)) # 784 = 28 * 28
B1 = tf.Variable(tf.zeros([L]))
W2 = tf.Variable(tf.truncated_normal([L, M], stddev=0.1))
B2 = tf.Variable(tf.zeros([M]))
# W3 = tf.Variable(tf.truncated_normal([M, N], stddev=0.1))
# B3 = tf.Variable(tf.zeros([N]))
# W4 = tf.Variable(tf.truncated_normal([N, O], stddev=0.1))
# B4 = tf.Variable(tf.zeros([O]))
W5 = tf.Variable(tf.truncated_normal([M, TAEGET_NUM], stddev=0.1))
B5 = tf.Variable(tf.zeros([TAEGET_NUM]))
# The model
XX = tf.reshape(X, [-1, 784])
Y1 = tf.nn.sigmoid(tf.matmul(XX, W1) + B1)
Y2 = tf.nn.sigmoid(tf.matmul(Y1, W2) + B2)
# Y3 = tf.nn.sigmoid(tf.matmul(Y2, W3) + B3)
# Y4 = tf.nn.sigmoid(tf.matmul(Y3, W4) + B4)
Ylogits = tf.matmul(Y2, W5) + B5
Y = tf.nn.softmax(Ylogits)
# cross-entropy
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=Y_, logits=Ylogits))
我们选取两个隐藏层的神经元个数分别为300和150(且Adam的学习率为0.003时),看看效果。200次迭代的效果如下,训练和测试的准确度分别为87%和83%,还没有上一篇文章的好呢?

再看下1000次迭代的效果为95%和81%,也是不及上一篇文章。
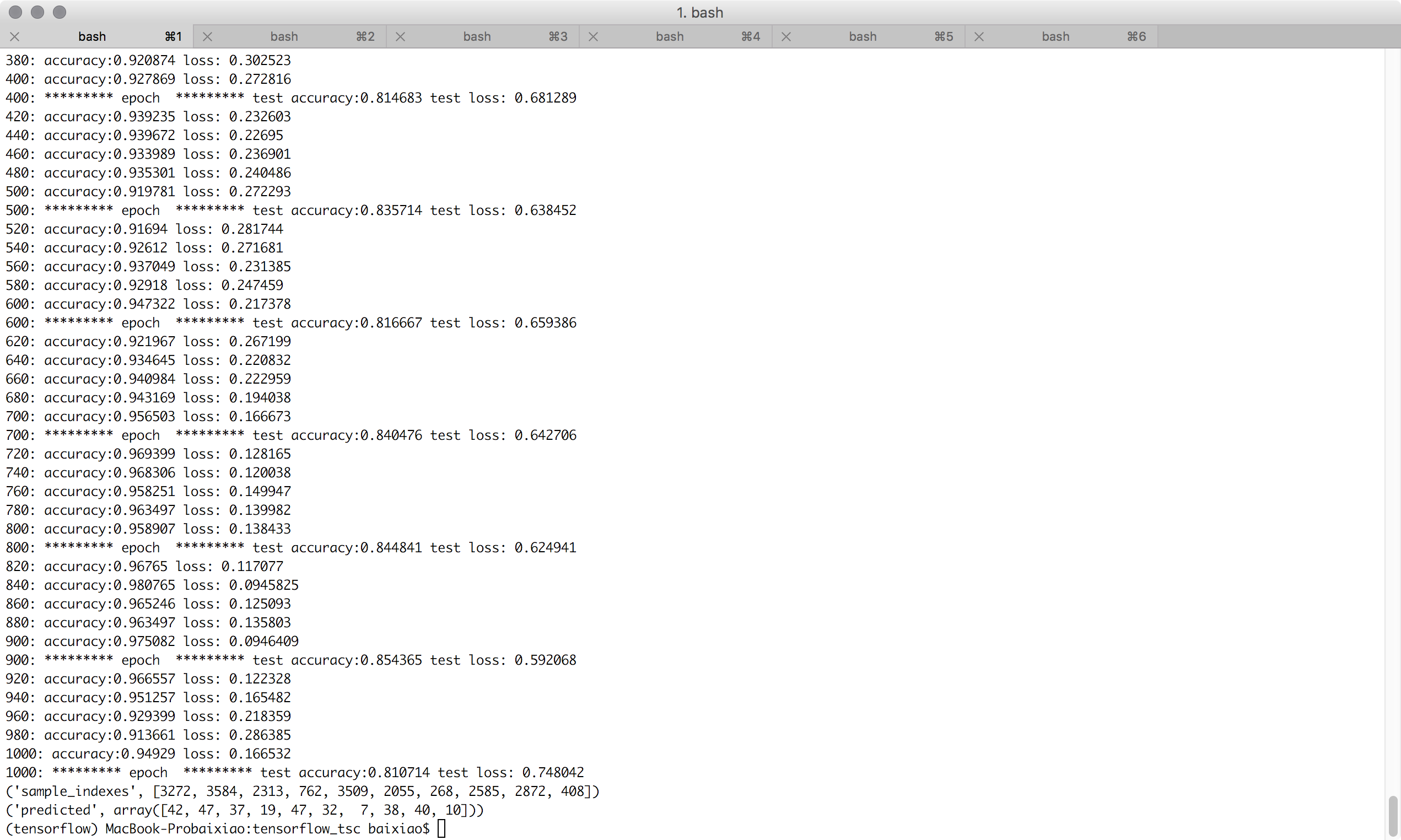
经过多次尝试,将两个隐藏层的神经元个数调整为为500和250(且Adam的学习率为0.002时),达到了最优效果。这也说明机器学习的调参是很重要的。调整后的效果如下:
200次迭代,测试准确度达到98%,测试准确度达到85.6%:

1000次迭代早早的测试准确度达到100%,测试准确度停留在87.6%:
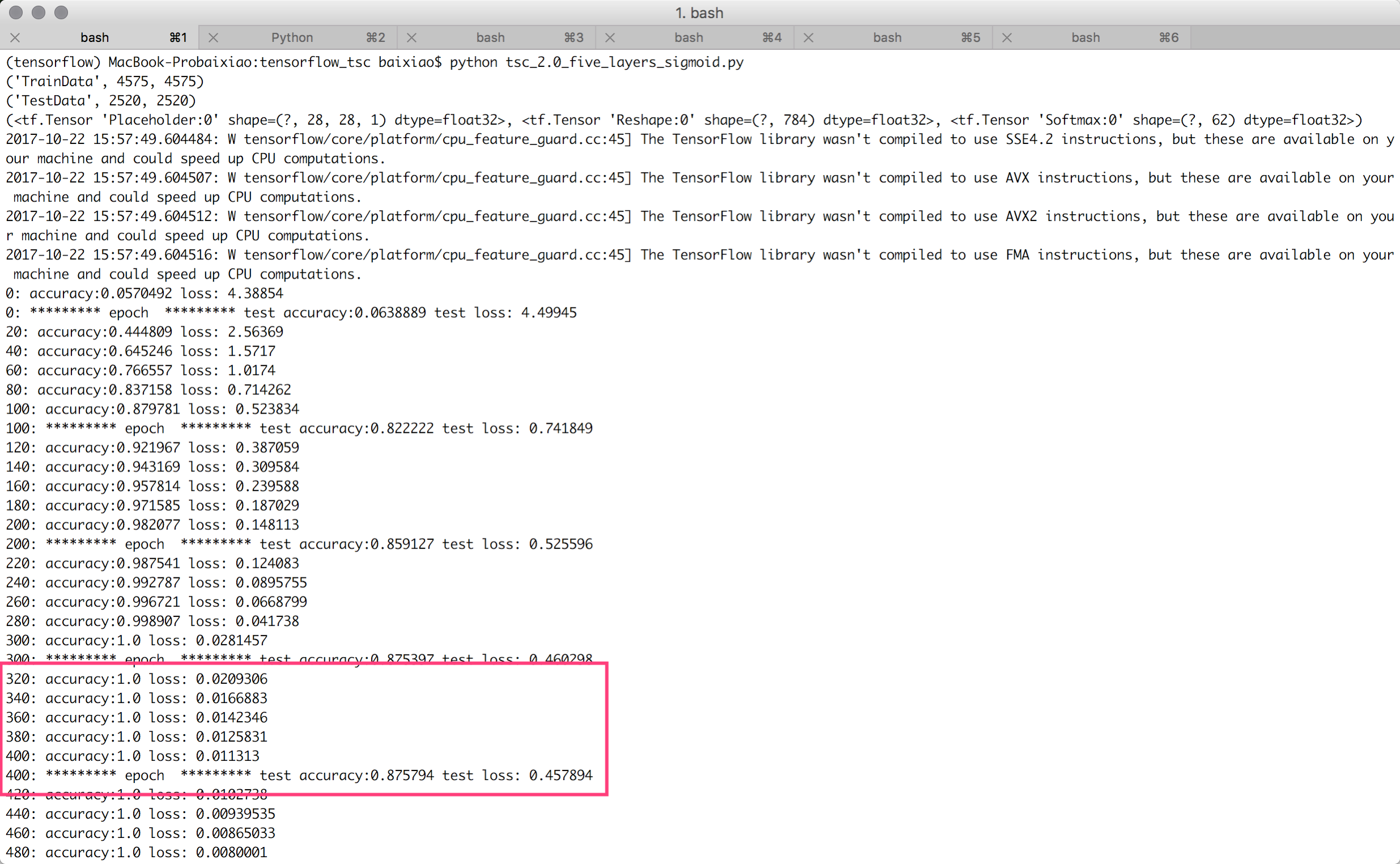
学习速率衰退

把上面1000次迭代的效果看完,你会发现从500次开始,测试数据的准确度和loss都在震荡。这是学习率过大的表现。但我们不能仅仅将学习率除以十或者永远不停地做训练。一个好的解决方案是开始很快随后将学习速率指数级衰减至比如说 0.001。代码如下:
# variable learning rate
lr = tf.placeholder(tf.float32)
# training step, learning rate will decay
train_step = tf.train.AdamOptimizer(lr).minimize(cross_entropy)
# You can call this function in a loop to train the model
def training_step(i, update_test_data, update_train_data):
batch_X, batch_Y = train.next_batch(BATCH_NUM)
# learning rate decay
max_learning_rate = 0.002
min_learning_rate = 0.001
decay_speed = 1000.0
learning_rate = min_learning_rate + (max_learning_rate - min_learning_rate) * math.exp(-i/decay_speed)
# compute training values for visualisation
if update_train_data:
a, c = sess.run([accuracy, cross_entropy], feed_dict={X: batch_X, Y_: batch_Y})
print(str(i) + ": accuracy:" + str(a) + " loss: " + str(c))
# compute test values for visualisation
if update_test_data:
test_X, test_Y = test.next_batch()
a, c = sess.run([accuracy, cross_entropy], feed_dict={X: test_X, Y_: test_Y})
print(str(i) + ": ********* epoch " + " ********* test accuracy:" + str(a) + " test loss: " + str(c))
# the backpropagation training step
sess.run(train_step, feed_dict={X: batch_X, Y_: batch_Y, lr: learning_rate})
可见,1000次迭代把准确度提升到88.7%,且准确度没有在震荡:
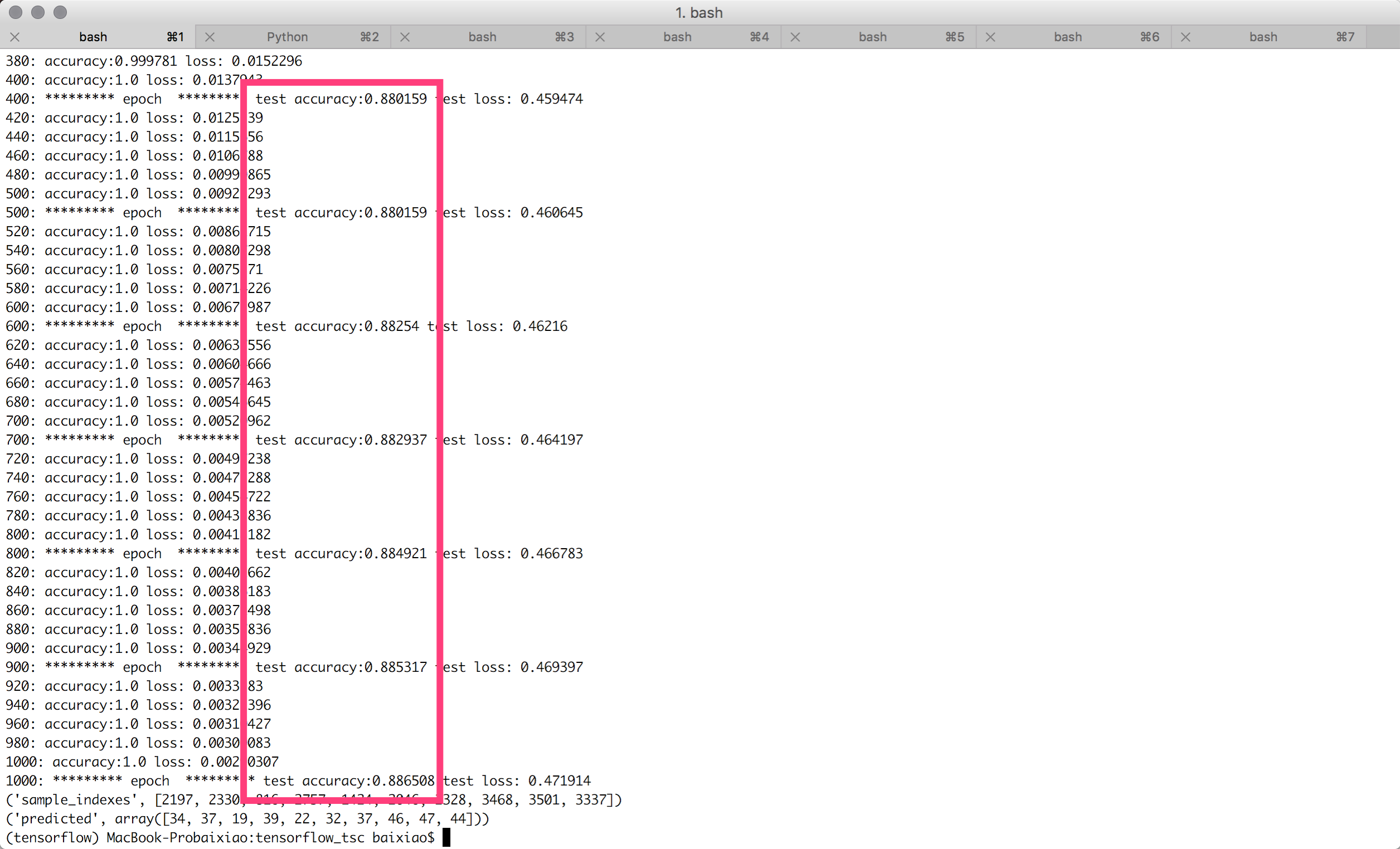
特别说明:通常情况下,我们工程中发现,3层神经网络效果优于2层神经网络,但是如果把层数再不断增加(4,5,6层),对最后结果的帮助就没有那么大的跳变了。不过在卷积神经网上还是不一样的,深层的网络结构对于它的准确率有很大的帮助,直观理解的方式是,图像是一种深层的结构化数据,因此深层的卷积神经网络能够更准确地把这些层级信息表达出来。摘自此文,且我的实验过程也是如此
结束
完整代码在https://github.com/baixiaoustc/tensorflow_tsc/blob/master/tsc_2.0_five_layers_sigmoid.py 以及 https://github.com/baixiaoustc/tensorflow_tsc/blob/master/tsc_2.1_five_layers_sigmoid_lrdecay.py
参考:
http://blog.csdn.net/han_xiaoyang/article/details/50447834
