用Tensorflow识别交通标志4:卷积神经网络

卷积网络
- 卷积网络的引入原因（深度网络的不足）
- 卷积神经网络的组成层
实战

手机阅读会有问题-。=

本文在前文：深层神经网络的基础上，引入卷积神经网络来继续提升交通标志图像识别的准确度。

卷积网络

卷积网络的引入原因（深度网络的不足）

前文提到的深层神经网络结构都比较一致，输入层和输出层中间夹着数层隐藏层，每一层都由多个神经元组成，层和层之间是全连接的结构，同一层的神经元之间没有连接。上面这种结构实际应用起来有较大的困难：就拿CIFAR-10举例吧，图片已经很小了，是 32 * 32 * 3 (长宽各32像素，3个颜色通道)的，那么在神经网络当中，我们只看隐藏层中的一个神经元，就应该有 32 * 32 * 3 = 3072 个权重，如果大家觉得这个权重个数的量还行的话，再设想一下，当这是一个包含多个神经元的多层神经网（假设n个），再比如图像的质量好一点（比如是 200 * 200 * 3 的），那将有 200 * 200 * 3 * n = 120000 * n 个权重需要训练，结果是拉着这么多参数训练，基本跑不动，跑得起来也是『气喘吁吁』，当然，最关键的是这么多参数的情况下，分分钟模型就过拟合了

另一个原因是，前文的模型中，都是对图像输入进行了flatten操作，即将图像的二维数组结构降维到一维来进行处理，那么图像的平面信息都被忽略掉了。实际上我们人类自己看图像时，肯定是对整个图像平面进行识别，而不是“一行一行地读取图像像素信息”。因此我们需要提取二维平面的信息。

卷积神经网络的组成层

在卷积神经网络中，有3种最主要的层：

卷积运算层
池化层
全连接层

另有“激活函数层”没有单独说明了。每一层的输入结构是3维的数据，计算完输出依旧是3维的数据。卷积层和全连接层包含训练参数，RELU和池化层不包含。卷积层，全连接层和池化层包含超参数，RELU层没有。下面具体说说每种层的结构。

卷积层

卷积层当然是最重要的层。

直观来讲，解释卷积层的最佳方法是想象有一束手电筒光正从图像的左上角照过。假设手电筒光可以覆盖 3 x 3 的区域，想象一下手电筒光照过输入图像的所有区域。这束手电筒被叫做过滤器（filter），被照过的区域被称为感受野（receptive field）。现在，以过滤器所处在的第一个位置为例，即图像的左上角。当筛选值在图像上滑动（卷积运算）时，过滤器中的值会与图像中的原始像素值相乘（又称为计算点积）。这些乘积被加在一起（从数学上来说，一共会有 27 个乘积，假设是3个颜色通道）。现在你得到了一个数字。切记，该数字只是表示过滤器位于图片左上角的情况。我们在输入图片上的每一位置重复该过程。（下一步将是将过滤器右移 1 单元，接着再右移 1 单元，以此类推。）输入内容上的每一特定位置都会产生一个数字。

结合神经元的概念，在卷积层中，假设该卷积层的『厚度』为2（为了和整个网络模型的『深度』作区分，特命名为厚度），则『每一片』上面的神经元共享同样的权重，即上面提到的过滤器。相比前文中每个神经元都有自己的权重，现在这种做法大大减少了权重的个数。卷积神经网络中每一层的神经元只会和上一层的一些局部区域相连，这就是所谓的局部连接性。直观来看卷积过程图：

继续介绍两个概念：步长/stride 和填充/padding

所谓步长/stride，是指的窗口从当前位置到下一个位置，『跳过』的中间数据个数。比如从图像数据层输入到卷积层的情况下，也许窗口初始位置在第1个像素，第二个位置在第5个像素，那么stride=5-1=4。大家可以发现一点，窗口滑动步长设定越小，两次滑动取得的数据，重叠部分越多，但是窗口停留的次数也会越多，运算量大一些；窗口滑动步长设定越长，两次滑动取得的数据，重叠部分越少，窗口停留次数也越少，运算量小。如下图是stride=2的情况：

所谓填充/padding，是在原始数据的周边补值的圈数。填充这个操作产生的根本原因是，为了保证窗口的滑动能从头刚好到尾。填充的策略，有直接填0，也有填相邻值的。如下图是padding=1的情况：

完整的包含步长/stride 和填充/padding的卷积过程：

数学是怎么计算的呢？如下图，设置该卷积层的『厚度』为2，故有两个过滤器为W1和W2（均为三维矩阵），故输出也是三维矩阵 3 * 3 * 2。

怎么感性地认识这些过滤器呢？每个过滤器都是对某种特征感兴趣，有的是直线，有的是曲线，有的是颜色，有的是形状，如下图：

池化层

池化层是夹在连续的卷积层中间的层。它的作用也非常简单，就是逐步地压缩/减少数据和参数的量，也在一定程度上减小过拟合的现象。池化层做的操作也非常简单，就是将原数据上的区域压缩成一个值(区域最大值/MAX或者平均值/AVERAGE)，最常见的池化设定是，将原数据切成2*2的小块，每块里面取最大值作为输出，这样我们就自然而然减少了75%的数据量。其实就是下采样：

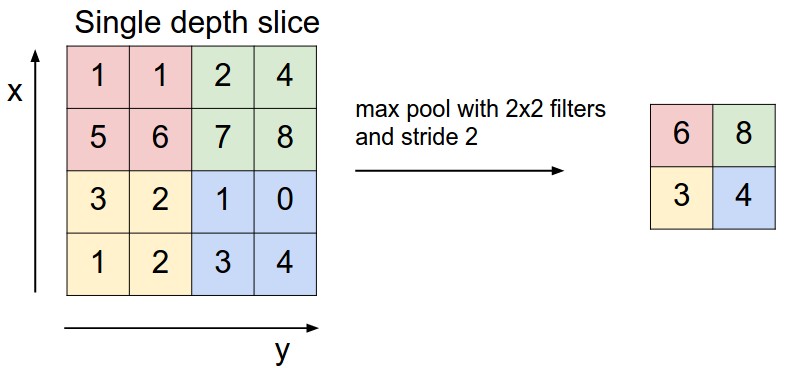
以上是max-pooling的操作。

全连接层

卷积网络最后一层通常是全联接层，和普通的神经网络相同，用于softmax最后计算分类。

实战

搭建卷积网络

回到我们具体的任务中，搭建一个卷积网络如下：

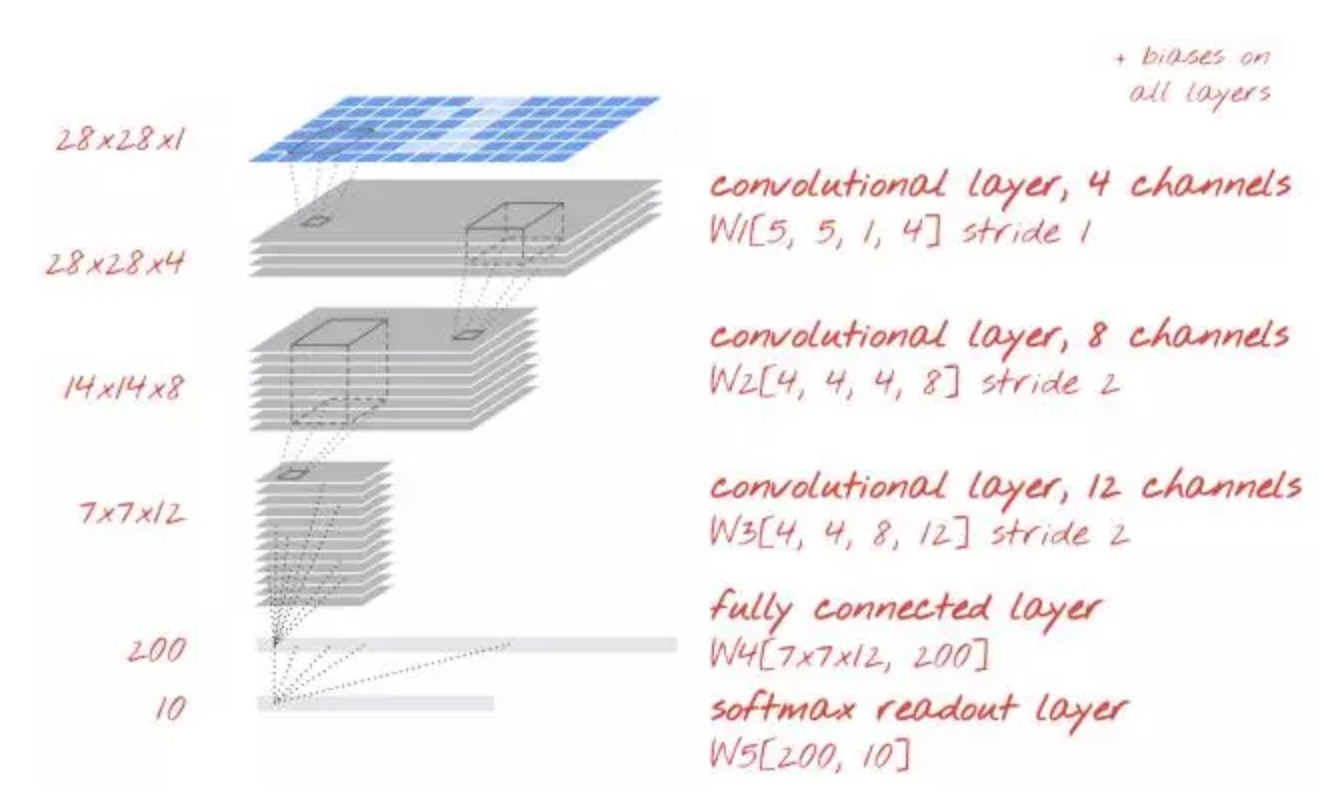
为了将我们的代码转化为卷积模型，我们需要为卷积层定义适当的权重张量，然后将该卷积层添加到模型中。我们已经理解到卷积层需要以下形式的权重张量。下面代码是用 TensorFlow 语法来对其初始化：

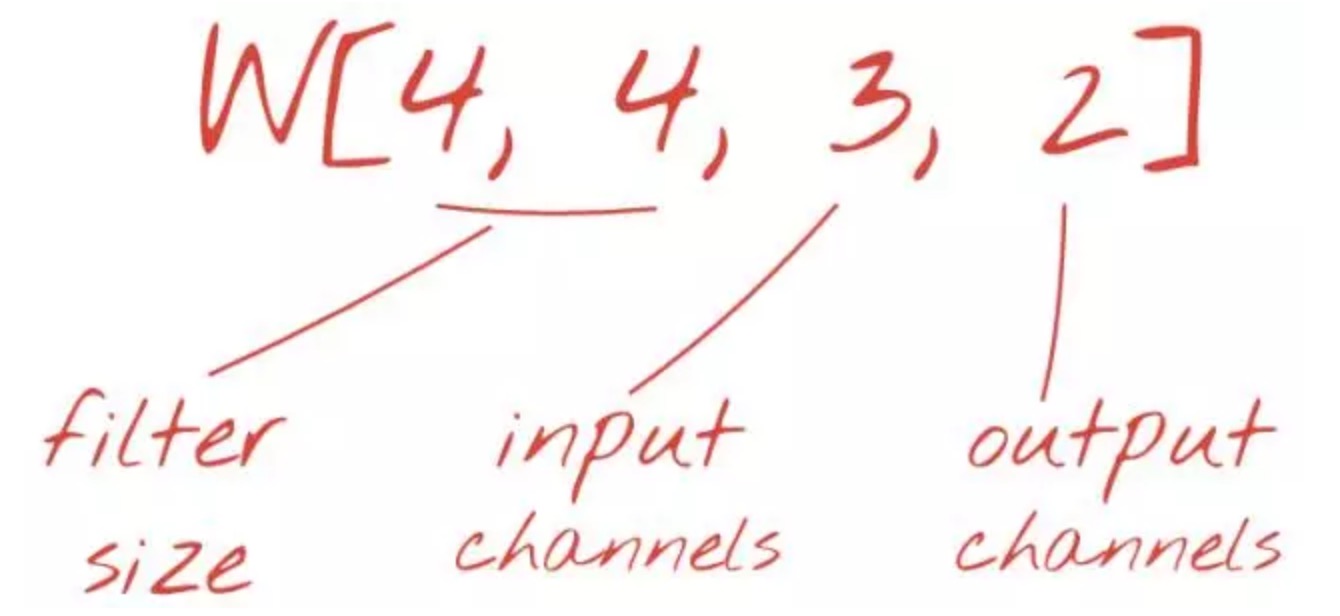
W = tf.Variable(tf.truncated_normal([4, 4, 3, 2], stddev=0.1))
B = tf.Variable(tf.ones([2])/10) # 2 is the number of output channels

在 TensorFlow 中，使用 tf.nn.conv2d 函数实现卷积层，该函数使用提供的权重在两个方向上扫描输入图片。这仅仅是神经元的加权和部分，你需要添加偏置单元并将加权和提供给激活函数。

stride = 1  # output is still 28x28
Ycnv = tf.nn.conv2d(X, W, strides=[1, stride, stride, 1], padding='SAME')
Y = tf.nn.relu(Ycnv + B)

我们再来看看运算步骤：

200次迭代(cnn+sigmoid)，测试准确度达到100%，测试准确度达到87.5%：

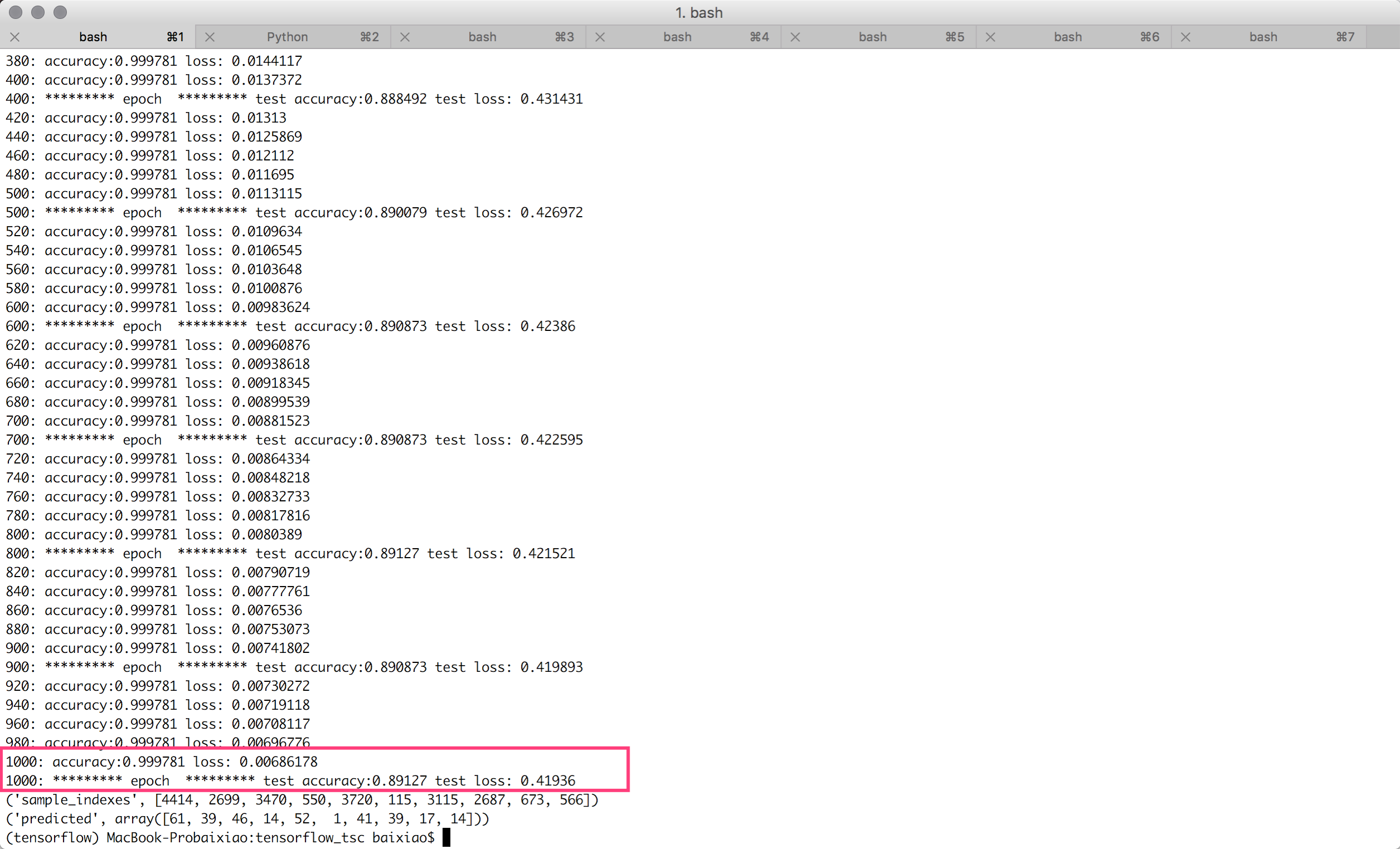
增加到1000次，测试准确度只提高到88.1%，估计是过拟合了：

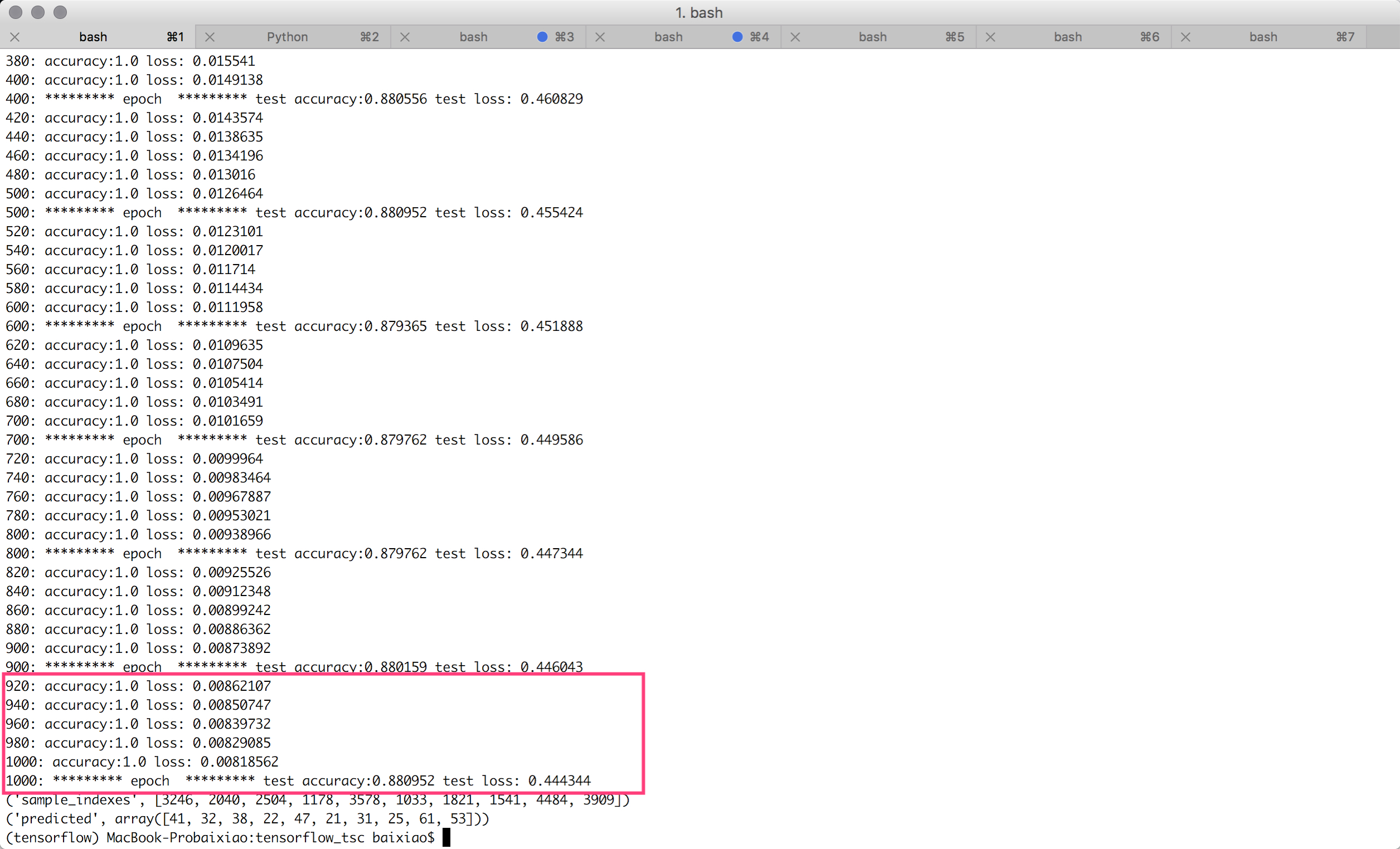
完整代码在https://github.com/baixiaoustc/tensorflow_tsc/blob/master/tsc_3.0_convolutional.py

过拟合和dropout

从上面的实验看到，测试准确度很早的达到了100%，但是测试数据这边没有提升。这是过拟合的表现，学习算法只是在训练数据上做工作并相应地优化训练的交叉熵，它再也看不到测试数据了。

它不会立刻影响你模型对于真实世界的识别能力，但是它会使你运行的众多迭代毫无用处，而且这基本上是一个信号——告诉我们训练已经不能再为模型提供进一步改进了。这种无法连接通常会被标明「过拟合（overfitting）」，而且当你看到这个的时候，你可以尝试采用一种规范化（regularization）技术，称之为「dropout」。

在 dropout 里，在每一次训练迭代的时候，你可以从网络中随机地放弃一些神经元。你可以选择一个使神经元继续保留的概率 pkeep，通常是 50% 到 75% 之间，然后在每一次训练的迭代时，随机地把一些神经元连同它们的权重和偏置一起去掉。在一次迭代里，不同的神经元可以被一起去掉（而且你也同样需要等比例地促进剩余神经元的输出，以确保下一层的激活不会移动）。当测试你神经网络性能的时候，你再把所有的神经元都装回来 (pkeep=1)。

TensorFlow 提供一个 dropout 函数可以用在一层神经网络的输出上。它随机地清零一些输出并且把剩下的提升 1/pkeep。这里是如何把它用在一个两层神经网络上的例子。

# feed in 1 when testing, 0.75 when training
pkeep = tf.placeholder(tf.float32)

Y1 = tf.nn.relu(tf.matmul(X, W1) + B1)
Y1d = tf.nn.dropout(Y1, pkeep)

Y = tf.nn.softmax(tf.matmul(Y1d, W2) + B2)

200次迭代(cnn+0.75的dropout)，测试准确度达到88.7%：

1000次迭代(cnn+0.75的dropout)，测试准确度达到89.1%，还是没能突破90%：

完整代码在https://github.com/baixiaoustc/tensorflow_tsc/blob/master/tsc_3.1_convolutional_dropout.py

超越90%

我们还有什么信息没有用到，使得目前准确度还是没有突破90%？是彩色！回到我们这个任务来，交通标志很明显的是和颜色相关的，绿色或者红色对交通标志的含义很明显。我们需要在图片预处理的时候不再做颜色单一化操作，使得输入数据的颜色通道变为3，故相应的 placeholder 的维度都要相应变化：

# input X: 28x28 color images, the first dimension (None) will index the images in the mini-batch
X = tf.placeholder(tf.float32, [None, 28, 28, 3])

W1 = tf.Variable(tf.truncated_normal([5, 5, 3, K], stddev=0.1))  # 5x5 patch, 3 input channel, K output channels

200次终于突破90%！！！