动态规划
动态规划(dynamic programming,简称 dp),是一类求解最优值的算法。有一定的套路可以遵循。
特点
《牛逼了,原来大神都是这样学动态规划的…》文章总结的:
动态规划是一种多阶段决策最优解模型,一般用来求最值问题,多数情况下它可以采用自下而上的递推方式来得出每个子问题的最优解(即最优子结构),进而自然而然地得出依赖子问题的原问题的最优解。
包含三个特点:
- 多阶段决策:是指原问题可以拆分成子问题以及子子问题
- 最优子结构:是指子问题的最优解可以推导为原问题的最优解
- 自下而上:由子问题到上层问题之间,寻找迭代递推公式,也叫「状态转移方程」
特别说明一下,「自下而上」区别于递归算法的「自上而下」,后者的子问题可能存在大量的重叠,导致大量的重复计算,这样时间复杂度很可能呈指数级上升。这个从后面的例子可以看出。
套路
怎么判断题目可以使用动态规划
根据上述特点,当问题的定义是求最值问题,且问题可以采用递归的方式,并且递归的过程中有大量重复子问题的时候,基本可以断定问题可以用动态规划求解。故此基本套路是:
- 判断是否可用递归来解
- 分析在递归的过程中是否存在大量的重复子问题
- 采用备忘录的方式来存子问题的解以避免大量的重复计算(剪枝)
- 改用自底向上的方式来递推,即动态规划
状态转移方程
实际中写出「状态转移方程」是最困难的,《动态规划详解(修订版)》文章给出了一个套路:
明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base case
下面我们用零钱兑换问题来实践上面的套路。
零钱兑换问题
这是 LeetCode 的322题:
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。
1,递归解法
递归的关键是看问题能否拆分成子问题,并且是否有临界条件。
一,定义递归函数,函数的功能是给定 coins 列表和 amount,返回凑硬币的最少个数:
func exchangeRecursive(coins []int, amount int) int {
}二,寻找问题与子问题的关系,即递推公式。推导过程如下:
函数记为 f(coins, amount)。假设选择了第一枚硬币,则需要对剩余的 amount - coins[0] 金额求最少硬币数:
f(coins, amount) = f(coins, amount-coins[0]) + 1 (这里的 1 代表选择了第一枚硬币)
如果选择了第二,第三枚呢,递推公式如下:
f(coins, amount) = f(coins, amount-coins[1]) + 1 (这里的 1 代表选择了第二枚硬币)
f(coins, amount) = f(coins, amount-coins[2]) + 1 (这里的 1 代表选择了第三枚硬币)
选择最优解,递归公式如下:
f(coins, amount) = min{f(coins, amount - coins[i]) + 1)}, 其中 i 的取值为所有硬币的序号
三,逻辑补充到递归函数
//递归函数,返回凑硬币的最小个数,不能凑的情况返回-1
func exchangeRecursive(coins []int, amount int) int {
//两个临界条件
if amount == 0 {
return 0
}
if amount < 0 {
return -1
}
//因为是求最小值,所以先初始化为极大值
var result int = math.MaxInt32
for _, coin := range coins {
ret := exchangeRecursive(coins, amount-coin)
if ret == -1 {
continue
}
result = int(math.Min(float64(result), float64(ret)+1))
}
if result == math.MaxInt32 {
return -1
}
return result
}
func coinChangeRecursive(coins []int, amount int) int {
return exchangeRecursive(coins, amount)
}分析时间复杂度,由下图递归树可知为多叉树,是 O(n^k),k 是硬币个数,总之是指数级别的。
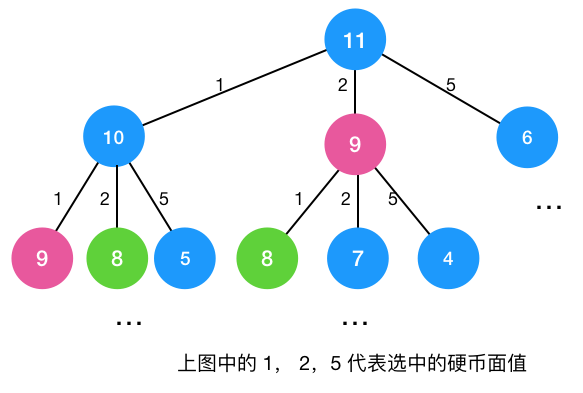
自测通过,但是提交代码超时。分析可知递归解法存在大量重叠子问题,导致的大量重复计算,如上图中,节点9和节点8都被计算了两次,而且每个节点下面都可能是一颗巨大的子树。
2,递归剪枝解法
既然存在重叠子问题,则引入备忘录的方式来存储中间结果。实际中选择数组而不是字典来存储,能提升一点效率:
func coinChangeCut(coins []int, amount int) int {
m := make([]int, amount+1)
for i := 0; i <= amount; i++ {
m[i] = math.MaxInt32
}
return exchangeCut(coins, amount, m)
}
//递归函数,加剪枝
func exchangeCut(coins []int, amount int, m []int) int {
if amount == 0 {
return 0
}
if amount < 0 {
return -1
}
//存储中间结果
if m[amount] != math.MaxInt32 {
return m[amount]
}
var result int = math.MaxInt32
for _, coin := range coins {
ret := exchangeCut(coins, amount-coin, m)
if ret == -1 {
continue
}
result = int(math.Min(float64(result), float64(ret)+1))
}
if result == math.MaxInt32 {
result = -1
}
m[amount] = result
return result
}如下图对比可知,剪枝后减少了大量计算量。时间复杂度降至 O(nk) 。

3,动态规划解法
前文推导递归公式如下:
f(coins, amount) = min{f(coins, amount - coins[i]) + 1)}, 其中 i 的取值为所有硬币的序号
按照动态规划的套路,需要明确「状态」和「选择」。定义 dp[n] 为凑够零钱金额 n 需要的最小硬币值,此为状态。选择某一个硬币,此为选择。则状态转移方程如下:
dp[n] = min{dp[n - coins[i]] + 1} = min{dp[n - coins[i]]} + 1, 其中 i 的取值为所有硬币的序号
以示例1为例(示例 1: 输入: coins = [1, 2, 5], amount = 11),我们只要自底向上根据以上状态转移方程依次求解 dp[1], dp[2], dp[3] …… dp[11],最终的 dp[11],即为我们所求的解。数学公式表达为:

再注意初始状态是 dp[0] = 0,表示金额为0的方法为0种。
func coinChangeDP(coins []int, amount int) int {
dp := make([]int, amount+1) //dp[i]表示amount为i时的最优解
for i := 0; i <= amount; i++ {
dp[i] = math.MaxInt32
}
//init
dp[0] = 0
for _, coin := range coins {
for i := coin; i <= amount; i++ {
//状态转移方程
dp[i] = int(math.Min(float64(dp[i]), float64(dp[i-coin]+1)))
}
}
if dp[amount] == math.MaxInt32 {
return -1
}
return dp[amount]
}下图就很直观了:

小结
回头来看,可以看到零钱兑换问题符合之前定义的动态规划问题特点,即可以拆分子问题、符合最优子结构、自下而上存在状态转移方程。
首先用普通迭代解法,存在大量重复计算;接着用剪枝消除重叠子问题;最后用动态规划解法。
其实我们来看动态规划解法的 dp[] 数组,和迭代剪枝解法中的备忘录结构是一样的,不同在于自下而上还是自顶而下的方向。
