背包问题
背包问题是动态规划中一个子类。
01背包问题
问题描述:
有 n 个物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?
问题分析:
定义一些变量:Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,背包问题抽象化(X1,X2,…,Xn,其中 Xi 取0或1,表示第 i 个物品选或不选)。注意,每个物品只能最多拿一次,这也是01叫法的来源。
- 建立模型,即求max(V1X1+V2X2+…+VnXn);
- 寻找约束条件,W1X1+W2X2+…+WnXn < capacity;
举个例子:
n = 3, capacity = 4
weight = [2, 1, 3]
value = [4, 2, 3]
应该返回6,选择前两个物品。
二维DP
根据之前《动态规划套路》,先明确「状态」,比较浅显的一种描述是「状态」是二维的,分别对应「可选的物品」和「背包的容量」,即 dp[i][j] 表示前 i 个物品的组合在容量 j 的背包的最大价值。
再明确「选择」,很显然就是要不要第 i 个物品,根据选择情况,思考状态转移方程。对于第 i 个物品,如果不选择它,那么当前状态和前 i-1 个物品的状态一致:
dp[i][j] = dp[i-1][j]
如果要选择它,那么从当前状态倒推上一个状态是 dp[i-1][j-weight[i],它们的关系是:
dp[i][j] = dp[i-1][j-weight[i]]+value[i]
求最值:
dp[i][j] = max{dp[i-1][j], dp[i-1][j-weight[i]]+value[i]}
再考虑初始条件,对于容量大于等于第一个物品的情况,值都是第一个物品的价值。
func knapsackZeroOne2DP(weight []int, value []int, capacity int) int {
length := len(weight)
if length == 0 || length != len(value) {
return 0
}
//普通背包解法
//dp[i][j],表示前i个组合,其容量和为j的最大价值
dp := make([][]int, length)
for i := range dp {
dp[i] = make([]int, capacity+1)
}
//init
for j := range dp[0] {
if weight[0] <= j {
dp[0][j] = value[0]
}
}
for i := 1; i < length; i++ {
for j := 0; j <= capacity; j++ {
//如果不选第i个物品
dp[i][j] = dp[i-1][j]
if j >= weight[i] {
//如果要选的话
dp[i][j] = int(math.Max(float64(dp[i-1][j]), float64(dp[i-1][j-weight[i]]+value[i])))
}
}
}
return dp[length-1][capacity]
}一维DP
再回头看看前面的状态转移方程:
dp[i][j] = max{dp[i-1][j], dp[i-1][j-weight[i]]+value[i]}
可以考虑优化空间复杂度。从knapsackZeroOne2DP的代码也可以看出来,是经历了两重循环,每一轮的外层循环 i,算出二维 DP 的其中一行 dp[i][0..capacity],且 dp[i][j] 仅与 dp[i-1][j], dp[i-1][j-weight[i]] 相关,即该行数据仅与前面一行 i-1 相关。那么可以把二维数据缩减为一维,dp[j] 的定义为容量 j 的背包的最大价值,总结01背包的套路如下:
for i=1..N;
for j=capacity..0;
dp[j]=max{dp[j],dp[j-weight[i]]+value[i]};
注意内部循环为降序,降序的理解是:为了保证 j-weight[i] 是「上一层」的状态,即 i 还在上一个循环的状态,即 j 在 j-weight[i] 的前面。画图加深理解:

//01背包问题,1维dp
func knapsackZeroOne1DP(weight []int, value []int, capacity int) int {
length := len(weight)
if length == 0 || length != len(value) {
return 0
}
//高级背包解法
//dp[j],表示容量和为i的最大价值
dp := make([]int, capacity+1)
//init,容量为0,价值为0
dp[0] = 0
for i := 0; i < length; i++ {
for j := capacity; j >= weight[i]; j-- {
//照搬公式
dp[j] = int(math.Max(float64(dp[j]), float64(dp[j-weight[i]]+value[i])))
}
}
return dp[capacity]
}时间复杂度并不会变。
示例
来看看 LeetCode 的416题《分割等和子集》:
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意:
每个数组中的元素不会超过 100
数组的大小不会超过 200
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2:
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.
使用01背包的套路,根据题意,所有数字的总和肯定是个偶数,且总和的一半记为 sum,sum 就是背包问题的容量,dp[j] 定义为容量为 j 时的能分割的可能性。状态转移方程替换为:
dp[j] = dp[j] || dp[j-nums[i]]
想一想怎么理解?再考虑初始条件,如果 sum 为0,解法为 true。
func canPartitionZeroOne(nums []int) bool {
length := len(nums)
if length == 0 || length > 200 {
return false
}
sum := 0
for _, n := range nums {
sum += n
}
if sum%2 != 0 || sum > 200*100 {
return false
}
sum = sum / 2
//高级背包解法
//dp[i],表示和为i的可能性
dp := make([]bool, sum+1)
//init
dp[0] = true
for i := 0; i < length; i++ {
for j := sum; j >= nums[i]; j-- {
dp[j] = dp[j] || dp[j-nums[i]]
}
}
return dp[sum]
}完全背包问题
问题描述:
有 n 种物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?注意每种物品都有无限件可用。
问题分析:
和01背包问题相比,不同的是有无限件可用。
二维DP
按照套路,先定义状态。dp[i][j] 表示前 i 种物品的组合在容量 j 的背包的最大价值。由于每种物品可以选择0件或多件,可以定义状态转移方程如下:
dp[i][j] = max{dp[i-1][j], dp[i-1][j-weight[i]]+value[i], dp[i-1][j-2*weight[i]]+2*value[i], ... , dp[i-1][j-k*weight[i]]+k*value[i]} (满足 j >= k*weight[i]) 【公式1】
一维DP
同样考虑空间优化。定义状态,dp[j] 的定义为容量 j 的背包的最大价值。数学公式推导一下:
设 j = j-weight[i],带入【公式1】:
dp[i][j-weight[i]] = max{dp[i-1][j-weight[i]], dp[i-1][j-2*weight[i]]+value[i], dp[i-1][j-3*weight[i]]+2*value[i], ... , dp[i-1][j-k*weight[i]]+(k-1)*value[i]} (满足 j >= k*weight[i]) 【公式2】
将【公式1】和【公式2】合并:
dp[i][j] = max{dp[i-1][j], dp[i][j-weight[i]]+value[i]}
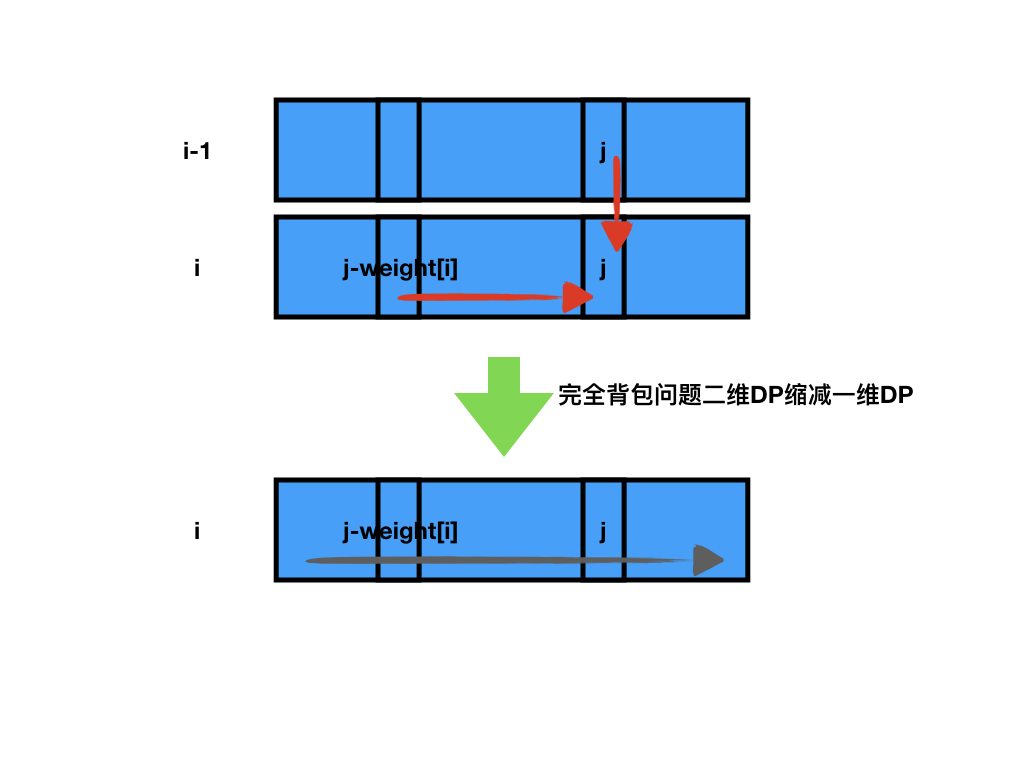
可见 dp[i][j] 只和上一层的状态 dp[i-1][j] 以及本层的前置状态 dp[i][j-weight[i]] 相关,故可以缩减为一维数组:
dp[j] = max{dp[j], dp[j-weight[i]]+value[i]}
总结完全背包的套路如下:
for i=1..N;
for j=0..capacity;
dp[j]=max{dp[j],dp[j-weight[i]]+value[i]};
注意内部循环为升序,为了保证 j-weight[i] 是「本层」的状态,即保证 j 依赖 j-weight[i],j 在 j-weight[i] 的后面。
注意完全背包的套路和01背包几乎完全一样,只是内循环的顺序颠倒了。区别就在于01背包依赖的两个项都是「上一层」的状态,而完全背包依赖了「上一层」和「本层」的状态
画图加深理解:
示例
前文的《零钱兑换》问题,就是每种硬币可以使用无限次。所以可以使用完全背包的套路,来解零钱兑换问题。考虑初始条件后,代码和前文动态规划的代码基本一致。代码略。
另一个示例,来看看 LeetCode 的518题《零钱兑换II》:
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
输入: amount = 10, coins = [10]
输出: 1
注意:
你可以假设:
0 <= amount (总金额) <= 5000
1 <= coin (硬币面额) <= 5000
硬币种类不超过 500 种
结果符合 32 位符号整数
使用完全背包的套路,只不过根据本题题意,将状态转移方程替换为:
dp[j] = dp[j] + dp[j-weight[i]]
再考虑初始条件,如果 amount 为0,则只有一种组合情况为「空」。
//完全背包解法
func change(amount int, coins []int) int {
dp := make([]int, amount+1)
//init
dp[0] = 1
for _, coin := range coins {
for i := coin; i <= amount; i++ {
dp[i] += dp[i-coin]
}
}
return dp[amount]
}